cho hình vẽ 2 , biết\(A_1=B_1\)và \(C_1=D_1\). chứng minh \(m\perp b\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
ND
Những câu hỏi liên quan
Cho hình vẽ 2, biết
\(A_1=B_1\)và \(C_1=C_2\). chứng minh\(m\perp b\)
Cho lục giác lồi ABCDEF. Gọi \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF,FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh đối diện song song và bằng nhau.
Cho lục giác lồi ABCDEF, gọi các điểm \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF, FEA, FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh song song và bằng nhau.
Cho lục giác lồi ABCDEF. Gọi \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF,FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh đối diện song song và bằng nhau.
Cho lục giác lồi ABCDEF, gọi các điểm \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF, FEA, FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh song song và bằng nhau.
Cần chứng minh
\(\overrightarrow{A_1B_1}=\overrightarrow{E_1D_1}\), \(_{ }\overrightarrow{B_1C_1}=\overrightarrow{F_1E_1}\), \(\overrightarrow{C_1D_1}=\overrightarrow{A_1F_1}\)
Ta có :
\(\overrightarrow{OA_1}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\) ; \(\overrightarrow{OD_1}=\frac{\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}}{3}\)
\(\overrightarrow{OB_1}=\frac{\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}}{3}\) ; \(\overrightarrow{OE_1}=\frac{\overrightarrow{OE}+\overrightarrow{OF}+\overrightarrow{OA}}{3}\)
Từ đó suy ra :
\(\overrightarrow{A_1B_1}+\overrightarrow{OD_1}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}}{3}=\overrightarrow{0B_1}+\overrightarrow{OE_1}\)
và do đó
\(\overrightarrow{A_1B_1}=\overrightarrow{E_1D_1}\)
Tương tự ta cũng có \(\overrightarrow{B_1C_1}=\overrightarrow{F_1E_1}\) ,\(\overrightarrow{C_1D_1}=\overrightarrow{A_1F_1}\) => Điều phải chứng minh
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD có đáy là hình bình hành và C_1 là trung điểm SC. Mặt phẳng (P) tùy ý chứa A C_1 cắt các cạnh SB,SD lần lượt tại B_1,D_1. a)Chứng minh rằng: frac{SB}{SB_1}+frac{SD}{SD_1}3b) Xác định vị trí của (P) để tam giác SB_1D_1có diện tích bé nhất
Đọc tiếp
cho hình chóp S.ABCD có đáy là hình bình hành và \(C_1\) là trung điểm SC. Mặt phẳng (P) tùy ý chứa A \(C_1\) cắt các cạnh SB,SD lần lượt tại \(B_1,D_1\).
a)Chứng minh rằng: \(\frac{SB}{SB_1}+\frac{SD}{SD_1}=3\)
b) Xác định vị trí của (P) để tam giác \(SB_1D_1\)có diện tích bé nhất
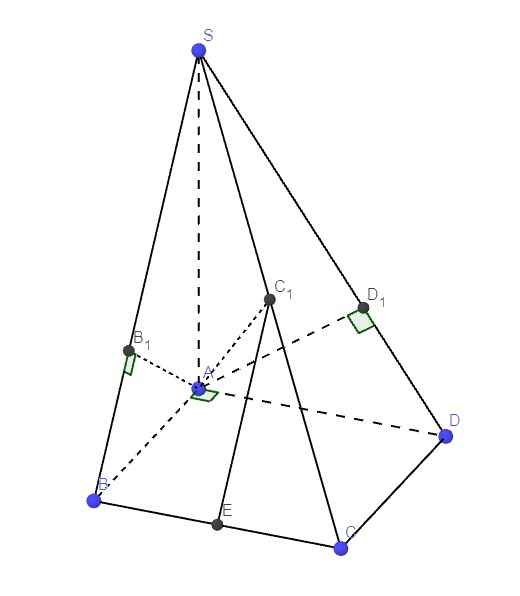
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy. Gọi B_1; C_1; D_1 là hình chiếu vuông góc của A lên các cạnh SB, SC, SD.a) Chứng minh rằng B_1D_1 // BD và SC ⊥ (AB_1D_1)b) Chứng minh rằng các điểm A, B_1, C_1, D_1 đồng phẳng và tứ giácAB_1C_1D_1 nội tiếp đường tròn.c) Cho SAasqrt{2}. Tính góc giữa hai đường thẳng SB và AC_1.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy. Gọi \(B_1\); \(C_1\); \(D_1\) là hình chiếu vuông góc của A lên các cạnh SB, SC, SD.
a) Chứng minh rằng \(B_1D_1\) // BD và SC ⊥ (A\(B_1D_1\))
b) Chứng minh rằng các điểm A, \(B_1\), \(C_1\), \(D_1\) đồng phẳng và tứ giác
A\(B_1C_1D_1\) nội tiếp đường tròn.
c) Cho SA\(=a\sqrt{2}\). Tính góc giữa hai đường thẳng SB và A\(C_1\).
a.
\(\Delta_VSAB=\Delta_VSAD\left(c.g.c\right)\Rightarrow AB_1=AD_1\)
\(\Rightarrow SB_1=SD_1\Rightarrow\dfrac{SB_1}{SB}=\dfrac{SD_1}{SD}\)
\(\Rightarrow B_1D_1||BD\) (Talet đảo)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AB_1\)
\(\Rightarrow AB_1\perp\left(SBC\right)\Rightarrow AB_1\perp SC\)
Hoàn toàn tương tự: \(AD_1\perp\left(SCD\right)\Rightarrow AD_1\perp SC\)
\(\Rightarrow SC\perp\left(AB_1D_1\right)\)
b.
\(\left\{{}\begin{matrix}SC\perp AC_1\\SC\perp\left(AB_1D_1\right)\end{matrix}\right.\) \(\Rightarrow AC_1\in\left(AB_1D_1\right)\)
\(\Rightarrow\) 4 điểm \(A;B_1;C_1;D_1\) đồng phẳng
Theo chứng minh câu a, \(AB_1\perp\left(SBC\right)\Rightarrow AB_1\perp B_1C_1\) (1)
\(AD_1\perp\left(SCD\right)\Rightarrow AD_1\perp\left(D_1C_1\right)\)
\(\Rightarrow B_1;D_1\) cùng nhìn \(AC_1\) dưới 1 góc vuông nên tứ giác \(AB_1C_1D_1\) nội tiếp đường tròn đường kính \(AC_1\)
Đúng 1
Bình luận (0)
c.
Gọi E là trung điểm BC
\(\Rightarrow C_1E\) là đường trung bình tam giác SBC
\(\Rightarrow C_1E||SB\Rightarrow\widehat{SB;AC_1}=\widehat{\left(C_1E;AC_1\right)}=\widehat{AC_1E}\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{3}\)
\(C_1E=\dfrac{1}{2}SB=\dfrac{a\sqrt{3}}{2}\)
\(AE=\sqrt{AB^2+BE^2}=\sqrt{AB^2+\left(\dfrac{BC}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
\(\dfrac{1}{AC_1^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AC_1=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
Áp dụng định lý hàm cos cho tam giác \(AEC_1\):
\(cos\widehat{AC_1E}=\dfrac{AC_1^2+C_1E^2-AE^2}{2AC_1.C_1E}=0\Rightarrow\widehat{AC_1E}=90^0\)
Đúng 0
Bình luận (0)
1. Cho dfrac{a}{b+c}+dfrac{b}{c+a}+dfrac{c}{a+b}1chứng minh rằng dfrac{a^2}{b+c}+dfrac{b^2}{c+a}+dfrac{c^2}{a+b}0
2. Giả sử a_1,b_1,c_1,a_2,b_2,c_2là các số khác 0 thỏa mãn đk : dfrac{a_1}{a_2}+dfrac{b_1}{b_2}+dfrac{c_1}{c_2}0vàdfrac{a_2}{a_1}+dfrac{b_2}{b_1}+dfrac{c_2}{c_1}1
CMR : dfrac{a_2^2}{a^2_1}+dfrac{b_2^2}{b_1^2}+dfrac{c_2^2}{c_1^2}1
Mình còn không hiểu đề bài cho lắm vậy nên mong mọi người giúp mình
Thanks
Đọc tiếp
1. Cho \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=1\)chứng minh rằng \(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}=0\)
2. Giả sử \(a_1,b_1,c_1,a_2,b_2,c_2\)là các số khác 0 thỏa mãn đk : \(\dfrac{a_1}{a_2}+\dfrac{b_1}{b_2}+\dfrac{c_1}{c_2}=0\)và\(\dfrac{a_2}{a_1}+\dfrac{b_2}{b_1}+\dfrac{c_2}{c_1}=1\)
CMR : \(\dfrac{a_2^2}{a^2_1}+\dfrac{b_2^2}{b_1^2}+\dfrac{c_2^2}{c_1^2}=1\)
Mình còn không hiểu đề bài cho lắm vậy nên mong mọi người giúp mình
Thanks
1. Ta có \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=1\)
\(\Rightarrow\left(a+b+c\right)\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)=a+b+c\)
\(\Rightarrow\dfrac{a^2}{b+c}+\left(b+c\right)\left(\dfrac{a}{b+c}\right)+\dfrac{b^2}{c+a}+\left(c+a\right)\left(\dfrac{b}{c+a}\right)+\dfrac{c^2}{a+b}+\left(a+b\right)\left(\dfrac{c}{a+b}\right)=a+b+c\)
\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}+a+b+c=a+b+c\)
\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}=0\) (đpcm).
Đúng 0
Bình luận (0)
2. Ta có: \(\dfrac{a_1}{a_2}+\dfrac{b_1}{b_2}+\dfrac{c_1}{c_2}=0\)
\(\Rightarrow\dfrac{a_1b_2c_2+b_1a_2c_2+c_1a_2b_2}{a_2b_2c_2}=0\)
\(\Rightarrow a_1b_2c_2+b_1a_2c_2+c_1a_2b_2=0\)
Lại có: \(\dfrac{a_2}{a_1}+\dfrac{b_2}{b_1}+\dfrac{c_2}{c_1}=1\)
\(\Rightarrow\left(\dfrac{a_2}{a_1}+\dfrac{b_2}{b_1}+\dfrac{c_2}{c_1}\right)^2=1\)
\(\Rightarrow\dfrac{a_2^2}{a_1^2}+\dfrac{b_2^2}{b_1^2}+\dfrac{c_2^2}{c_1^2}+2\left(\dfrac{a_2b_2}{a_1b_1}+\dfrac{b_2c_2}{b_1c_1}+\dfrac{a_2c_2}{a_1c_1}\right)=1\)
Mặt khác: \(\dfrac{a_2b_2}{a_1b_1}+\dfrac{b_2c_2}{b_1c_1}+\dfrac{a_2c_2}{a_1c_1}=\dfrac{a_1b_2c_2+b_1a_2c_2+c_1a_2b_2}{a_1b_1c_1}=0\)
Vậy \(\dfrac{a_2^2}{a_1^2}+\dfrac{b_2^2}{b_1^2}+\dfrac{c_2^2}{c_1^2}=1\) (đpcm)
Đúng 0
Bình luận (0)
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ - \widehat {DAB}} \right) + \left( {180^\circ - \widehat {ABC}} \right) + \left( {180^\circ - \widehat {BCD}} \right) + \left( {180^\circ - \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ - \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ - 360^\circ \\\)
\(= 360^\circ \)
Đúng 0
Bình luận (0)