CMR: 2x3 - 3x2 - 3x + 2= 0. Có 3 nghiệm phân biệt
TQ
Những câu hỏi liên quan
Cho hàm số
y
-
2
x
3
+
3
x
2
-
1
có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình
2
x
3
-
3
x
2
+
2
m
có đúng 3 nghiệm phân biệt, tron...
Đọc tiếp
Cho hàm số y = - 2 x 3 + 3 x 2 - 1 có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình 2 x 3 - 3 x 2 + 2 m có đúng 3 nghiệm phân biệt, trong đó có 2 nghiệm lớn hơn 1 2
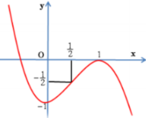
A. m ∈ - 1 2 ; 0
B. m ∈ - 1 ; 0
C. m ∈ 0 ; 1 2
D. m ∈ 1 4 ; 1 2
Tìm m để phương trình
2
x
3
-
3
x
2
+
1
m
có 3 nghiệm phân biệt: A.
0
≤
m
≤
1
B.
0
m
≤
1
C.
0
m
1
D.
0
≤
m
≤
1
Đọc tiếp
Tìm m để phương trình 2 x 3 - 3 x 2 + 1 = m có 3 nghiệm phân biệt:
A. 0 ≤ m ≤ 1
B. 0 < m ≤ 1
C. 0 < m < 1
D. 0 ≤ m ≤ 1
Đáp án C
Xét y = 2x3 – 3x2 + 1
Ta có: y’ = 6x2 – 6x
ð y’ = 0 ⇔ x = 0 hoặc x = 1
Ta có bảng biến thiên
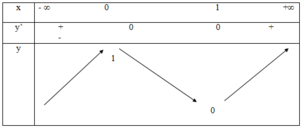
Số nghiệm phương trình đã cho m = 2x3 – 3x2 + 1
= Số giao điểm của đồ thị hàm số y = 2x3 – 3x2 + 1 và đường thẳng y = m
-> 0<m<1
Đúng 0
Bình luận (0)
Tập hợp các giá trị thực của tham số m để phương trình
2
x
3
-
3
x
2
-
12
x
+
2
m
-
1
0
có ba nghiệm phân biệt là: A.
-
3
;
21
2...
Đọc tiếp
Tập hợp các giá trị thực của tham số m để phương trình 2 x 3 - 3 x 2 - 12 x + 2 m - 1 = 0 có ba nghiệm phân biệt là:
A. - 3 ; 21 2
B. - 3 ; 21 2
C. - 3 ; + ∞
D. - ∞ ; 21 2
1) Tìm m để pt : -2x2 - 3x - m + 1 = 0 có 2 nghiệm âm phân biệt.
2) Tìm m để pt : -3x2 - 4x -2m + 1 = 0 có 2 nghiệm âm.
MN GIÚP E BÀI NÀY VỚI Ạ. E ĐANG CẦN GẤP Ạ.
\(1,\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(-3\right)^2-4\left(-2\right)\left(-m+1\right)>0\\x_1+x_2=\dfrac{3}{-2}< 0\\x_1x_2=\dfrac{-m+1}{-2}>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}17-8m>0\\-m+1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{17}{8}\\m>1\end{matrix}\right.\Leftrightarrow1< m< \dfrac{17}{8}\)
\(2,\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(-4\right)^2-4\left(-3\right)\left(-2m+1\right)\ge0\\x_1+x_2=\dfrac{4}{-3}< 0\\x_1x_2=\dfrac{-2m+1}{-3}>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}28-24m\ge0\\-2m+1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{7}{6}\\m>\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< m\le\dfrac{7}{6}\)
Đúng 2
Bình luận (1)
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt:
a) 3x2 - 3x + m - 2 = 0
b) (m - 5)x2 - x + 1 = 0
a: Δ=(-3)^2-4(m-2)
=9-4m+8
=17-4m
Đểphương trình có 2 nghiệm phân biệt thì -4m+17>0
=>-4m>-17
=>m<17/4
b: TH1: m=5
=>-x+1=0
=>x=1(loại)
TH2: m<>5
Δ=(-1)^2-4(m-5)
=1-4m+20=21-4m
Để phương trình có hai nghiệm phân biệt thì 21-4m>0
=>4m<21
=>m<21/4
Đúng 2
Bình luận (0)
Câu 48/Đề 7: Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] đêể bất phương trình log3(x2+x+1)+2x3 ≤ 3x2 + log3x +m-1 có ít nhất 2 nghiệm phân biệt
Có bao nhiêu giá trị thực của tham số m để phương trình
m
.
3
x
2
-
3
x
+
2
+
3
4
-
x
2
3
6
-...
Đọc tiếp
Có bao nhiêu giá trị thực của tham số m để phương trình m . 3 x 2 - 3 x + 2 + 3 4 - x 2 = 3 6 - 3 x + m 1 có đúng 3 nghiệm phân biệt
A.4
B.2
C.3
D.1
Cho phương trình x2 - 3x + m - 1 = 0 với m là tham số.
tim m để phương trình trên có 2 nghiệm phân biệt x1 , x2 sao cho 2x1 - 3x2 = 1
\(\text{Δ}=\left(-3\right)^2-4\left(m-1\right)=-4m+4+9=-4m+13\)
Để phương trình có hai nghiệm phân biệt thì -4m+13>0
hay m<13/4
Áp dụng Vi-et, ta được: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=3\\2x_1-3x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=2\\x_2=1\end{matrix}\right.\)
Theo đề, ta có: m-1=2
hay m=3(nhận)
Đúng 2
Bình luận (0)
Cho hàm số
f
(
x
)
x
3
-
3
x
2
+
2
có đồ thị là đường cong trong hình bên. Hỏi phương trình
x
3
-
3
x
2
+
2...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 3 x 2 + 2 có đồ thị là đường cong trong hình bên.
Hỏi phương trình
x
3
-
3
x
2
+
2
3
-
3
(
x
3
-
3
x
2
+
2
)
2
+
2
=
0
có bao nhiêu nghiệm thực phân biệt?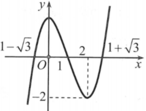
Chứng minh phương trình 2x3-9x2+12x-2-m=0 có 3 nghiệm dương phân biệt với mọi m thuộc (2;3)
Đặt \(f\left(x\right)=2x^3-9x^2+12x-2-m\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(\forall m\in\left(2;3\right)\) ta có:
\(f\left(0\right)=-2-m< 0\)
\(f\left(1\right)=3-m>0\)
\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (1)
\(f\left(2\right)=2-m< 0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (2)
\(f\left(3\right)=7-m>0\)
\(\Rightarrow f\left(2\right).f\left(3\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(2;3\right)\) (3)
Từ (1); (2); (3) \(\Rightarrow f\left(x\right)\) luôn có 3 nghiệm dương pb
Đúng 1
Bình luận (0)