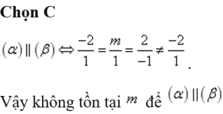d1 song song d2 khi:

\(\left\{{}\begin{matrix}m\ne0\\\frac{1}{m}=\frac{2m-1}{6}\ne\frac{m}{-3}\end{matrix}\right.\)

\(\frac{1}{m}=\frac{2m-1}{6}\Rightarrow2m^2-m-6=0\)

\(\Rightarrow\) Theo Viet \(m_1m_2=\frac{-6}{2}=-3\)

Đường tròn tâm \(I\left(3;-2\right)\) bán kính \(R=5\)

Áp dụng định lý Pitago: \(d\left(I;AB\right)=\sqrt{R^2-\left(\frac{AB}{2}\right)^2}=3\)

d' song song d nên pt có dạng: \(3x-4y+c=0\) (với \(c\ne-2\))

\(d\left(I;d'\right)=3\Leftrightarrow\frac{\left|3.3-4.\left(-2\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=3\)

\(\Leftrightarrow\left|c+17\right|=15\Rightarrow\left[{}\begin{matrix}c=-2\left(l\right)\\c=-32\end{matrix}\right.\)

Vậy pt d': \(3x-4y-32=0\)

b/ \(\Delta\) là tiếp tuyến (C) \(\Leftrightarrow d\left(I;\Delta\right)=R\)

\(\Leftrightarrow\frac{\left|3.3+4.\left(-2\right)+m\right|}{\sqrt{3^2+4^2}}=5\Leftrightarrow\left|m+1\right|=25\Rightarrow\left[{}\begin{matrix}m=24\\m=-26\end{matrix}\right.\)

Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}3x+4y+24=0\\3x+4y-26=0\end{matrix}\right.\)

c/ Thay tọa độ đường thẳng vào pt (C) được:

\(\left(3+2t\right)^2+\left(-2-t\right)^2-6\left(3+2t\right)+4\left(-2-t\right)-12=0\)

\(\Leftrightarrow5t^2-25=0\Rightarrow t=\pm\sqrt{5}\)

Tọa độ giao điểm: \(\left\{{}\begin{matrix}A\left(3+2\sqrt{5};-2-\sqrt{5}\right)\\B\left(3-2\sqrt{5};-2+\sqrt{5}\right)\end{matrix}\right.\)

1: x^2+y^2+6x-2y=0

=>x^2+6x+9+y^2-2y+1=10

=>(x+3)^2+(y-1)^2=10

=>R=căn 10; I(-3;1)

Vì (d1)//(d) nên (d1): x-3y+c=0

Theo đề, ta có: d(I;(d1))=căn 10

=>\(\dfrac{\left|-3\cdot1+1\cdot\left(-3\right)+c\right|}{\sqrt{1^2+\left(-3\right)^2}}=\sqrt{10}\)

=>|c-6|=10

=>c=16 hoặc c=-4

\(d_1\) nhận \(\left(m;1\right)\) là 1 vtpt

\(d_2\) nhận \(\left(1;-2\right)\) là 1 vtpt

Để \(d_1\) song song \(d_2\)

\(\Leftrightarrow\frac{m}{1}=\frac{1}{-2}\ne\frac{9}{m}\Rightarrow m=-\frac{1}{2}\)

a. Gọi \(A\left(x_0;y_o\right)\) là điểm cố định mà \(\Delta\)đi qua

Ta có phương trinh hoành độ giao điểm \(\left(m-3\right)x_o-\left(m-2\right)y_0+m-1=0\)

\(\Leftrightarrow mx_0-my_0+m-\left(3x_0-2y_0+1\right)=0\Leftrightarrow m\left(x_0-y_0+1\right)-\left(3x_0-2y_0+1\right)=0\)

Vì đẳng thức đúng với mọi m nên \(\hept{\begin{cases}x_0-y_0+1=0\\3x_0-2y_0-1=0\end{cases}\Rightarrow\hept{\begin{cases}x_0=3\\y_0=4\end{cases}\Rightarrow}A\left(3;4\right)}\)

Vậy \(\Delta\)luôn đi qua điểm \(A\left(3;4\right)\)cố định 

b. Ta có \(\left(m-2\right)y=\left(m-3\right)x+m-1\)

Để \(\Delta\)song song với Ox thì \(\hept{\begin{cases}m-2\ne0\\m-3=0\end{cases}\Rightarrow m=3}\)

Để \(\Delta\)song song với Oy thì \(\hept{\begin{cases}m-2=0\\m-3\ne0\end{cases}\Rightarrow m=2}\)

Để \(\Delta\)song song với đt \(y=x\)\(\Rightarrow\hept{\begin{cases}m-2=1\\m-3=1\end{cases}\Rightarrow\hept{\begin{cases}m=3\\m=4\end{cases}\left(l\right)}}\)

Vậy không tồn tại m để \(\Delta\)song song với đt \(y=x\)