trong hê tọa độ oxy, cho hình vuông ABCD. Trên tia đối AB lấy M (khác A), trên AD lấy N. Biết A(-1;5), M(3,9), N(3,-1), điểm E(1;1) thuộc đg thg BD. Tìm pt đg chéo BD
JE
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD, lấy điểm M trên đoạn BC, đường thẳng AM có phương trình x + 3y -5 = 0 , N trên đoạn CD sao cho góc BMA = AMN. Tìm tọa độ điểm A biết AN qua K(1;-2)
cho ABCD là hình vuông. Trên cạnh AD lấy điểm M, trên tia đối của tia AD lấy điểm N, trên tia đối của AB lấy điểm E sao cho DM= AN= BE. Vẽ hình vuông AMPQ ( Q thuộc cạnh AB). Chứng minh rằng MPEC là hình vuông
Cho hình thang ABCD, đáy nhỏ AB. Trên tia đối của tia AD lấy N sao cho AN=AD. Trên tia đối của tia BC lấy M sao cho BM=BC. Qua A kẻ đường vuông góc DM, cắt đường thẳng qua B vuông góc CN tại I. Chứng minh IC=ID.
1)tam giác ABC nhọn, trên tia đối AB lấy D sao cho AB=AD, trên tia đối AC lấy điểm M sao cho AC=AM . Tứ giác BCDM là hình j ? why ? 2) Cho tam giác ABC vuông tại A , biết AB=3cm, AC=4cm a) Tính AC b) Gọi M là trung điểm của BC, trên tia đối của MA lấy D sao cho MA=MD. Tứ giác ABCD là hình j ? why ?
Cho hình vuông ABCD có AB = 3cm
Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm
Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm
Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm
Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm
Chứng minh KLMN là hình vuông
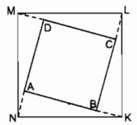
Xét △ ANK và △ BKL :
AN = BK (gt)
∠ A = ∠ B = 90 0
AK = BL (vì AB = BC, BK = CL)
Do đó △ ANK = △ BKL (c.g.c)
⇒ NK = KL (1)
Xét △ BKL và △ CLM:
BK = CL (gt)
∠ B = ∠ C = 90 0
BL = CM (vì BC = CD, CL = DM)
Do đó: △ BKL = △ CLM (c.g.c)
⇒ KL = LM (2)
Xét △ CLM và △ DMN :
CL = DM (gt)
∠ C = ∠ D = 90 0
CM = DN (vì CD = DA, DM = AN)
Do đó: △ CLM = △ DMN (c.g.c)
⇒ LM = MN (3)
Từ (1), (2) và (3) ⇒ NK = KL = LM = MN
Tứ giác MNKL là hình thoi
△ ANK = △ BKL ⇒ ∠ (ANK) = ∠ (BKL)
Trong tam giác ANK có A là góc vuông ⇒ ∠ (ANK) + ∠ (AKN) = 90 0
⇒ ∠ (BKL) + ∠ (AKN) = 90 0 hay ∠ (NKL) = 90 0
Vậy tứ giác MNKL là hình vuông.
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ oxy, cho hình vuông abcd có cạnh bằng 2. gọi m,n lần lượt là trung điểm của đoạn thẳng ab và c. trên đoạn mn lấy điểm h sao cho hm=3hn. lấy điểm i thuộc dường thẳng cd sao cho bi vuông góc với ah. biết c(1;1), d(5;3). tìm tọa độ điểm i
cho hình vuông ABCD . trên cạnh AB lấy điểm M tùy í. Dựng hình vuông ngoài hình ABCD hình vuông AMEF trên cạnh AD lấy điểm H và trên tia đối của tia BA lấy điểm K sao cho FH=MK=AB.
CM:EKCH là hình vuông
mk đang cần gấp. mn giúp mk nha
: Ký hiệu (a) là số đo góc a, đặt (CDK)=x
trên tia đối tia AB lấy điểm F sao cho AF = KC
như vậy tam giác ADF bằng tam giác CDK nên góc (ADF)=(CDK)=(KDE)=x
góc (FED)=(EDC)=2x (so le trong)
(FDE)=x+(90-2x)= 90-x
(EFD) = 180 - (FED) - (FDE) = 180 -( 2x) -(90-x) = 90-x = (FDE) vậy tam giác FED cân tại E hay DE =FE = FA +AE =KC + AE dpcm
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có AB = 3cm
Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm
Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm
Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm
Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm
Chứng minh KLMN là hình vuông
Cho hình bình hành ABCD , trên tia đối của tia DA lấy DM =AB , trên tia đối của tia BA lấy BN =AD
a) Chứng minh :ΔCBN∼ΔCDM cân
b)ΔCBN∼ΔMDC
c)Chứng minh M,C,N thẳng hàng



