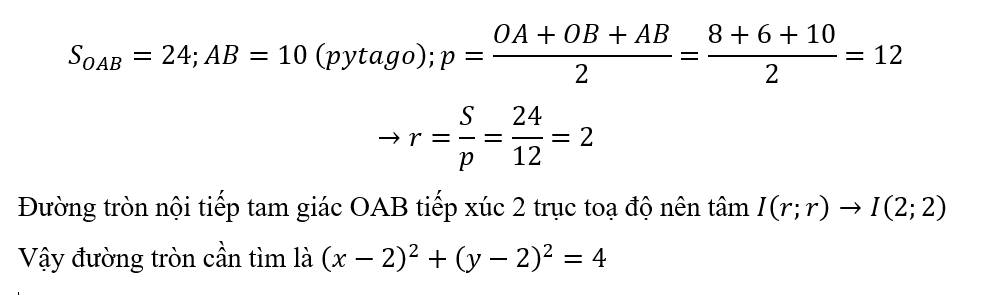Lập phương trình đường tròn nội tiếp tam giác OAB với A(-8,0), B(0,6)
LT
Những câu hỏi liên quan
Lập phương trình đường tròn nội tiếp tam giác OAB với A(8,0), B(0,6)
Cho hai điểm A(3;0), B(0;4). Đường tròn nội tiếp tam giác OAB có phương trình là A.
x
2
+
y
2
1
B.
x
2
+
y
2
-
2
x
-
2
y
+
1
0
C.
x...
Đọc tiếp
Cho hai điểm A(3;0), B(0;4). Đường tròn nội tiếp tam giác OAB có phương trình là
A. x 2 + y 2 = 1
B. x 2 + y 2 - 2 x - 2 y + 1 = 0
C. x 2 + y 2 - 6 x - 8 y + 25 = 0
D. x 2 + y 2 = 2
Cho 2 điểm A(3;0), B(0;4). Đường tròn nội tiếp tam giác OAB có phương trình là
Trong không gian Oxyz, cho hai điểm A ( 2;2;1 )
B
-
8
3
;
4
3
;
8
3
. Đường thẳng đi qua tâm đường tròn nội tiếp của tam giác OAB và vuông góc với mặt phẳng (OAB) có phương trình là A. ...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A ( 2;2;1 ) B - 8 3 ; 4 3 ; 8 3 . Đường thẳng đi qua tâm đường tròn nội tiếp của tam giác OAB và vuông góc với mặt phẳng (OAB) có phương trình là
A. x + 1 1 = y - 3 - 2 = z + 1 2
B. x + 1 1 = y - 8 - 2 = z - 4 2
C. x + 1 3 1 = y - 5 3 - 2 = z - 11 6 2
D. x + 2 9 1 = y - 2 9 - 2 = z + 5 9 2
Gọi I là tâm đường tròn ngoại tiếp ta tìm hai đường phân giác trong của tam giác rồi cho giao với nhau. (chú ý ở đây có kĩ thuật viết phương trình đường phân giác trong của tam giác trong không gian).
Đáp án cần chọn là A
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
(
2
;
2
;
1
)
;
B
-
8
3
;
4
3
;
8
3
.Đường thẳng đi qua tâm đường tròn nội tiếp của tam giác OAB và vuông góc với mặt...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A ( 2 ; 2 ; 1 ) ; B - 8 3 ; 4 3 ; 8 3 .Đường thẳng đi qua tâm đường tròn nội tiếp của tam giác OAB và vuông góc với mặt phẳng (OAB) có phương trình là:
A. x + 1 1 = y - 3 - 2 = z + 1 2
B. x + 1 1 = y - 8 - 2 = z - 4 2
C. x + 1 3 1 = y - 5 3 - 2 = z - 11 6 2
D. x + 2 9 1 = y - 2 9 - 2 = z + 5 9 2
Đáp án A.
![]()
Gọi I là tâm đường tròn nội tiếp tam giác OAB
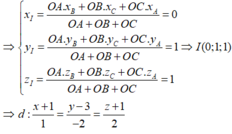
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
2
;
2
;
1
,
B
−
8
3
;
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 2 ; 2 ; 1 , B − 8 3 ; 4 3 ; 8 3 . Đường thẳng đi qua tâm đường tròn nội tiếp của tam giác OAB và vuông góc với mặt phẳng (OAB) có phương trình là:
A. x + 1 1 = y − 3 − 2 = z + 1 2 .
B. x + 1 1 = y − 8 − 2 = z − 4 2 .
C. x + 1 3 1 = y − 5 3 − 2 = z − 11 6 2 .
x + 2 9 1 = y − 2 9 − 2 = z + 5 9 2 .
Đáp án A
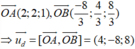
Gọi I là tâm đường tròn nội tiếp tam giác OAB
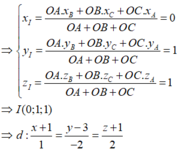
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
2
;
2
;
1
,
B
−
8
3
;
4
3
;
8
3
. Đường thẳng đi qua tâm đường tròn nội tiếp của...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 2 ; 2 ; 1 , B − 8 3 ; 4 3 ; 8 3 . Đường thẳng đi qua tâm đường tròn nội tiếp của tam giác OAB và vuông góc với mặt phẳng (OAB) có phương trình là
A. x + 1 1 = y − 3 − 2 = z + 1 2 .
B. x + 1 1 = y − 8 − 2 = z − 4 2 .
C. x + 1 3 1 = y − 5 3 − 2 = z − 11 6 2 .
D. x + 2 9 1 = y − 2 9 − 2 = z + 5 9 2 .
Đáp án A.
Ta có O E E ∈ A B Vecto chỉ phương
của đường thẳng (d) là u → = 1 ; − 2 ; 2 .
Kẻ phân giác O E E ∈ A B suy ra
O A O B = A E B E = 3 4 ⇒ A E → = 3 4 E B → ⇒ E 0 ; 12 7 ; 12 7 .
Gọi I là tâm đường tròn nội tiếp
Δ O A B ⇒ I ∈ O E ⇒ O I → = k O E , → với k > 0.
Tam giác OAB vuông tại O, có bán kính
đường tròn nội tiếp r = 1 ⇒ I O = 2 .
Mà
A E = 15 7 ; O A = 3 ; c os O A B ^ = 3 5 → O E = 12 2 7 s u y r a O E ¯ = 12 7 O I ¯ ⇒ I 0 ; 1 ; 1 .
Vậy phương trình đường thẳng cần tìm là
d : x + 1 1 = y − 3 − 2 = z + 1 2
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa đọ Oxy cho điểm Mleft(2;dfrac{3}{2}right)
a) Viết phương trình đường tròn (C) có đường kính OM
b) Viết phương trình đường thẳng d đi qua M và cắt hai nửa trục dương Ox, Oy lần lượt tại A, B sao cho diện tích tam giác OAB bằng 6 đơn vị diện tích
c) Tìm tọa độ tâm I của đường tròn nội tiếp (T) của tam giác OAB. Viết phương trình đường tròn đó
Đọc tiếp
Trong mặt phẳng tọa đọ Oxy cho điểm \(M\left(2;\dfrac{3}{2}\right)\)
a) Viết phương trình đường tròn (C) có đường kính OM
b) Viết phương trình đường thẳng d đi qua M và cắt hai nửa trục dương Ox, Oy lần lượt tại A, B sao cho diện tích tam giác OAB bằng 6 đơn vị diện tích
c) Tìm tọa độ tâm I của đường tròn nội tiếp (T) của tam giác OAB. Viết phương trình đường tròn đó
Trong không gian Oxyz, cho hai điểm A(1;0;1), B(-1;2;1). Viết phương trình đường thẳng D đi qua tâm đường tròn ngoại tiếp tam giác OAB và vuông góc với mặt phẳng (OAB). A.
x
t
y
1
+
t
z...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;0;1), B(-1;2;1). Viết phương trình đường thẳng D đi qua tâm đường tròn ngoại tiếp tam giác OAB và vuông góc với mặt phẳng (OAB).
A. x = t y = 1 + t z = 1 - t
B. x = t y = 1 + t z = 1 + t
C. x = 3 + t y = 4 + t z = 1 - t
D. x = - 1 + t y = t z = 3 - t