Cho hình vẽ biết BC//EF a) chứng minh AD//EF b)Tính góc BAE
MN làm giúp em trước 16:00, em cảm ơn ạ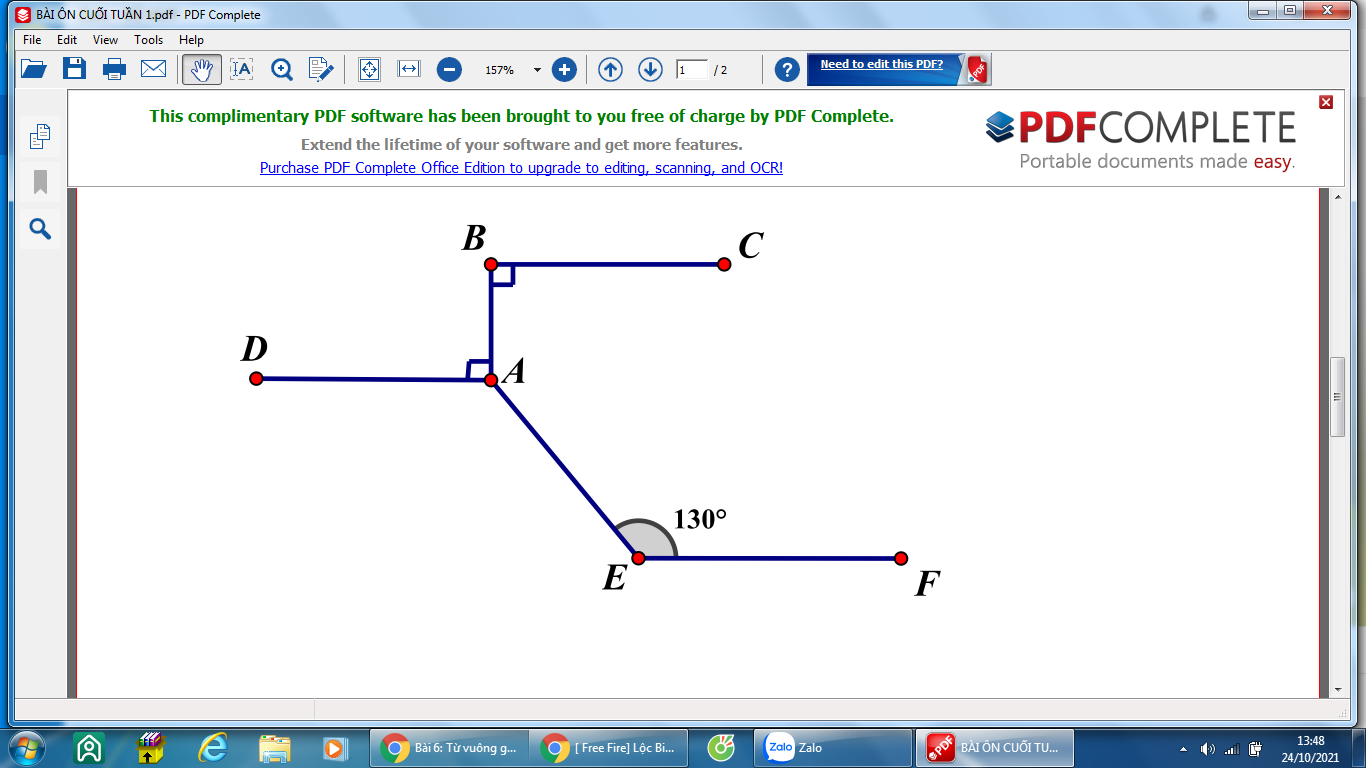
Cho hình vẽ biết BC//EF a) chứng minh AD//EF b)Tính góc BAE
MN làm giúp em trước 15:45, em cảm ơn ạ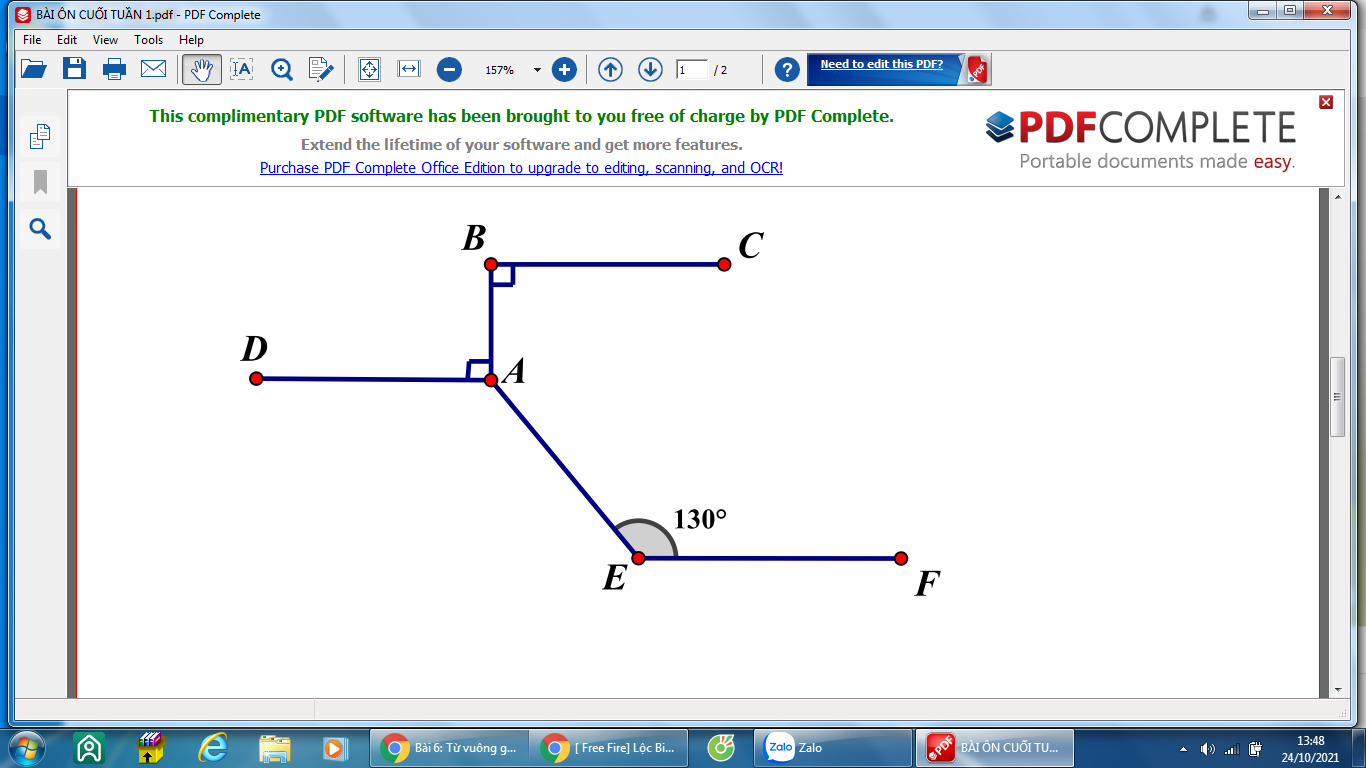
Cho hình vuông ABCD từ điểm M thuộc đường chéo BD kẻ ME vuông góc với AB và MF vuông góc với AD . chứng minh
a, DE=CF và DE vuông góc CF
b, CM =EF và CM vuông góc EF
GIẢI GIÚP EM VS Ạ EM CẢM ƠN
cho hình vẽ biết BC//EF a) chứng minh AD//EF b)Tính góc BAE
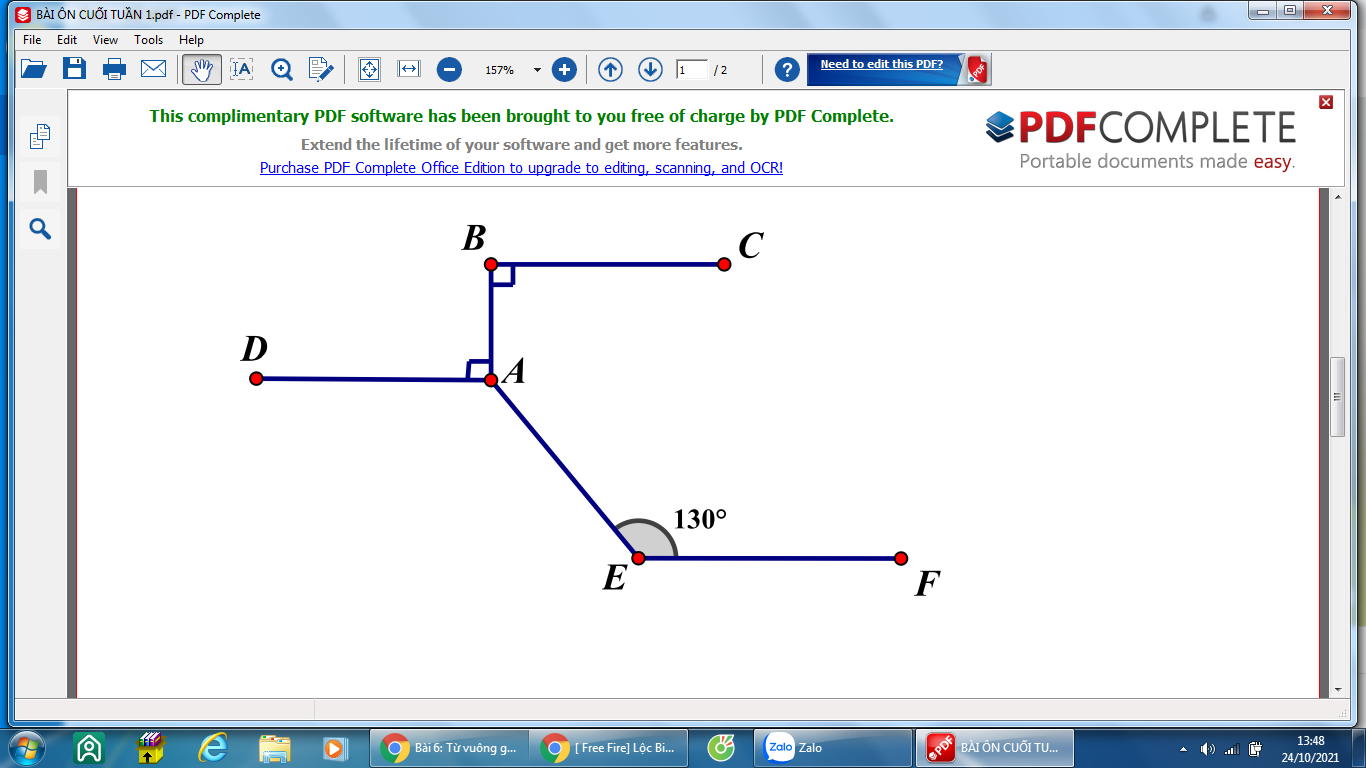
Mọi người vẽ hình + giải giúp em với ạ, em cảm ơn nhiều
Cho tam giác cân DEF (DE=DF), kẻ DE vuông góc với EF tại H
a, chứng minh HE=HF
b, giả sử xử DE = DF= 5 cm, EF = 8 cm Tính DH
c, gọi N và M lần lượt là trung điểm của DE và DF. Chứng minh EM = FN và Góc DEM = Góc DFN.
d, gọi giao điểm của EM và FN là K . Chứng minh tam giác KEF là tam giác cân
Sửa đề; DH vuông góc EF tại H
a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó: ΔDHE=ΔDHF
=>HE=HF
b: Ta có: HE=HF
H nằm giữa E và F
Do đó: H là trung điểm của EF
=>\(HE=HF=\dfrac{EF}{2}=4\left(cm\right)\)
ΔDHE vuông tại H
=>\(DH^2+HE^2=DE^2\)
=>\(DH^2=5^2-4^2=9\)
=>\(DH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: \(DM=MF=\dfrac{DF}{2}\)
\(DN=NE=\dfrac{DE}{2}\)
mà DF=DE
nên DM=MF=DN=NE
Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{MDE}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
=>EM=FN và \(\widehat{DEM}=\widehat{DFN}\)
d: Xét ΔNEF và ΔMFE có
NE=MF
NF=ME
EF chung
Do đó: ΔNEF=ΔMFE
=>\(\widehat{NFE}=\widehat{MEF}\)
=>\(\widehat{KEF}=\widehat{KFE}\)
=>ΔKEF cân tại K
Cho tam giác ABC nội tiếp đường tròn (O).3 đường cao AD,BE,CF cắt nhau ở H.(AB<AC).Chứng minh:
a,BCEF,AEHF là tứ giác nội tiếp.
b,2 đường thẳng BC,EF cắt nhau ở M.MA cắt đường tròn(O) ở I.Chứng minh AIFE là tứ giác nội tiếp.
c,Chứng minh :Góc AIH = 90 độ.
Em đang cần gấp ạ!Mọi người giúp em với ạ!Em cảm ơn mọi người trước ạ!
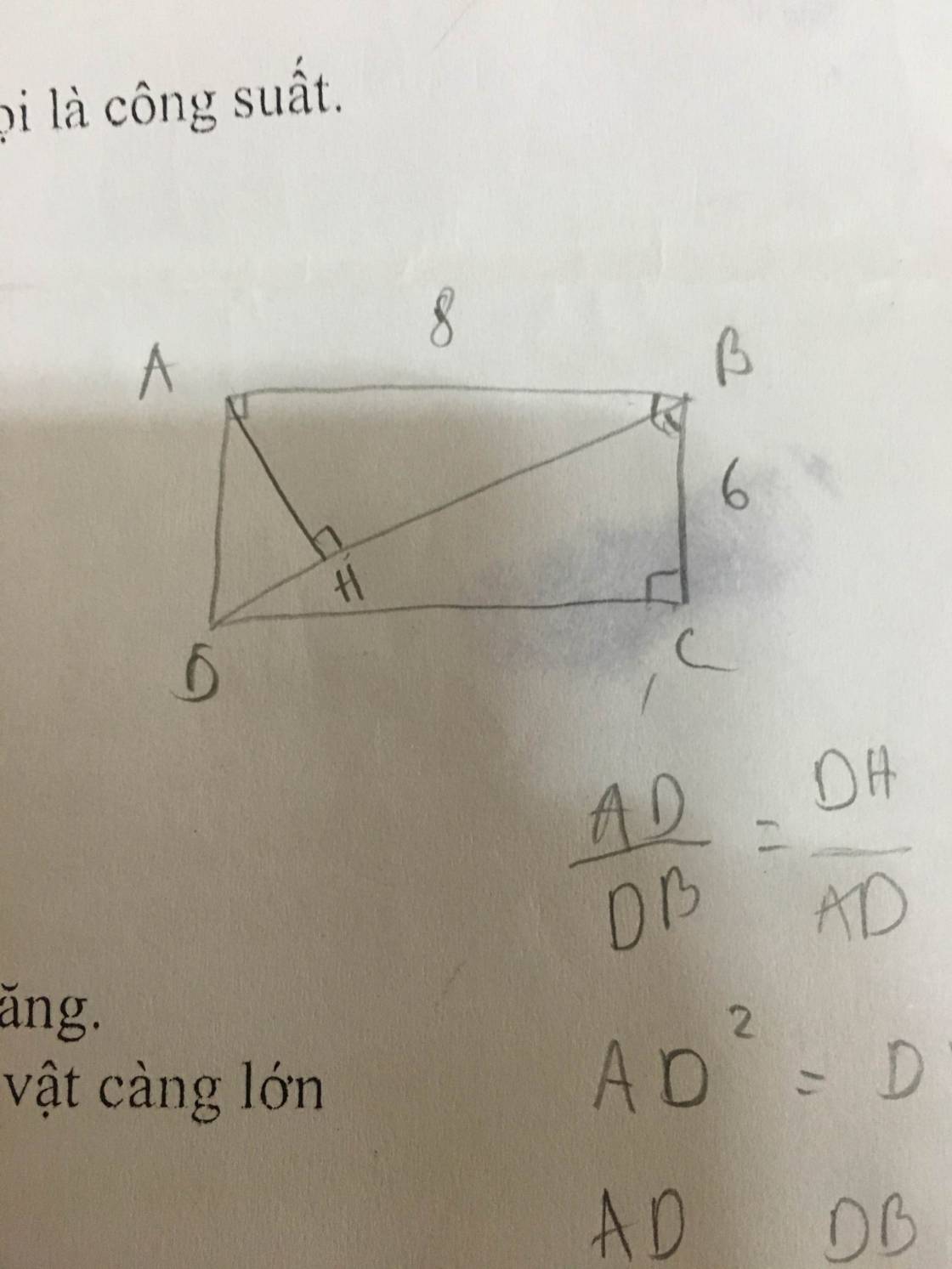
Mọi người giúp em làm bài toán hình này với ạ, kèm vẽ hình luôn nhé ạ. Em cảm ơn nhiều. - Cho hình chữ nhật ABCD có AB=8cm, BC= 6cm. Vẽ đường cao AH của tam giác ABD. a) chứng minh tam giác HBA đồng dạng với tam giác CDB b) Chứng minh: AD^2 = DH. DB c) Tính độ dài đoạn thẳng DH và AH
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
( sử dụng thước vẽ lại cho chính xác nhé. )
a. xét tam giác HBA và tam giác CDB, ta có :
góc B là góc chung ( gt )
góc H = góc D = 90 độ
do đó : tam giác HBA đồng dạng tam giác CDB ( g - g )
b.
• AD/DB = DH/BC
mà BC = AD ( vì ABCD là hcn )
nên AD/BD = DH/AD
= AD . AD = DB . DH
=> AD^2 = DB . DH ( đpcm )
• vì AB = DC ( ABCD là hcn )
nên DC = 8 cm
áp dụng định lý pytago trong tam giác DBC vuông tại C, ta có:
DB^2 = BC^2 + CD^2
DB^2 = 8^2 + 6^2
DB^2 = 64 + 36
DB^2 = 100
DB = căn bậc 2 của 100
DB = 10 ( cm )
vậy DB = 10 cm
Cho tam giác ABC cân tại A có AB=10cm, BC=12cm. Vẽ phân giác góc A cắt BC tại D
A, chứng minh tam giác ABD = tam giác ACM
B, tính AD, so sánh góc BAC và góc ABC
C, vẽ DE vuông góc AB (E thuộc AB) DF vuông góc AC (F thuộc AC). Chứng minh AF bằng AE và EF//BC.
Cho mình cả hình vẽ nha, minh cảm ơn
a) Ez bạn tự làm nha, mình làm sơ sơ cũng 3-4 cách rồi.:)
b) Tam giác ABC cân tại A có đường p/g góc A xuất phát từ đỉnh đồng thời là đường trung trực nên \(AD\perp BC\). và BD = CD = BC/2
Xét tam giác ABD vuông tại D (chứng minh trên), theo định lí Pythagoras:
\(AB^2=BD^2+DA^2\Leftrightarrow10^2=\frac{BC^2}{4}+DA^2\)
\(=36+DA^2\Rightarrow AD=8\) (cm) (khúc này có tính nhầm gì thì tự sửa lại nha!)
Theo đề bài ta có AB = AC = 10 < BC = 12
Hay AC < BC. Theo quan hệ giữa góc và cạnh đối diện trong tam giác ABC ta có \(\widehat{ABC}< \widehat{BAC}\) (Cái khúc này không chắc, sai thì thôi)
c) Hướng dẫn:
\(\Delta\)EDB = \(\Delta\)FDC (cạnh huyền - góc nhọn)
Suy ra EB = FC. Từ đó suy ra AE = AF.
Suy ra tam giác AEF cân tại A suy ra \(\widehat{AEF}=\frac{180^o-\widehat{A}}{2}\) (1)
Mặt khác tam giác ABC cân tại A nên \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra đpcm
Bài 1 : Cho tam giác ABC cân tại A vẽ AD ^ BC ( D thuộc BC)
a) Chứng minh BD = CD
b) Vẽ DH cắt AB tại H và DK cắt AC tại K . Chứng minh DH = Dk
c) Chứng minh HK // BC
d) Cho AB = 10 cm ; BC = 12 cm. Tính AD
Bài 2: Cho tam giác DEF có DE = DF = 5cm, EF= 6 cm . Gọi I là trung điểm của EF
a) Chứng minh tam giác DEI = tam giác DFI
b) Tính độ dài đoạn DI
c) Kẻ IH vuông góc với DE ( H thuộc DE) . Kẻ IJ vuông góc với DF ( J thuộc DF). Chứng minh : tam giác IHJ là tam giác cân
d) Chứng minh HJ song song EF
Mọi người ơi giúp em với ạ !
tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go
Cho hình bình hành ABCD, E thuộc AB, F thuộc AD. Đường thẳng qua D song song với EF cắt AC ở I. Đường thẳng qua B và song song với EF cắt AC ở k. Chứng minh :
a) AI =CK
b) AB/AE +AD/AF = AC/AN (N là giao điểm của EF và AC )
Ai giúp em vs ạ cảm ơn mn nhiều