Giải phương trình sau ( Đặt ẩn phụ ) :
( x² + x )² + 4( x² + x ) - 12 = 0
Giải các phương trình sau bằng cách đặt ẩn số phụ x - x - 1 -3 = 0
Đặt m = x - 1 .Điều kiện : m ≥ 0, x ≥ 1
Ta có : x - x - 1 -3 = 0 ⇔ (x -1) - x - 1 -2 =0
⇔ m 2 -m - 2 =0
Phương trình m 2 -m - 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng
a – b + c = 0
Suy ra : m 1 = -1 (loại) , m 2 = -(-2)/1 = 2
Với m =2 ta có: x - 1 =2 ⇒ x -1 =4 ⇔ x =5
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=5
Giải phương trình bằng cách đặt ẩn phụ:
x + 1 x 2 - 4 . x + 1 x + 3 = 0
x + 1 x 2 - 4 . x + 1 x + 3 = 0 Đ ặ t t = x + 1 x
(1) trở thành: t2 – 4t + 3 = 0 (2)
Giải (2):
Có a = 1; b = -4; c = 3
⇒ a + b + c = 0
⇒ (2) có nghiệm t1 = 1; t2 = c/a = 3.
+ t = 1 ⇒ x + 1/x = 1 ⇔ x2 + 1 = x ⇔ x2 – x + 1 = 0
Có a = 1; b = -1; c = 1 ⇒ Δ = (-1)2 – 4.1.1 = -3 < 0
Phương trình vô nghiệm.

Giải phương trình bằng cách đặt ẩn phụ:
a ) 2 x 2 − 2 x 2 + 3 x 2 − 2 x + 1 = 0 b ) x + 1 x 2 − 4 ⋅ x + 1 x + 3 = 0
a) 2 x 2 − 2 x 2 + 3 x 2 − 2 x + 1 = 0 ( 1 )
Đặt x 2 – 2 x = t ,
(1) trở thành : 2 t 2 + 3 t + 1 = 0 ( 2 ) .
Giải (2) :
Có a = 2 ; b = 3 ; c = 1
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = - 1 / 2 .
+ Với t = -1 ⇒ x 2 − 2 x = − 1 ⇔ x 2 − 2 x + 1 = 0 ⇔ ( x − 1 ) 2 = 0 ⇔ x = 1
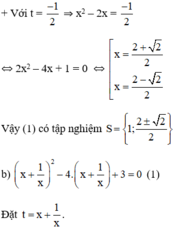
(1) trở thành: t 2 – 4 t + 3 = 0 ( 2 )
Giải (2):
Có a = 1; b = -4; c = 3
⇒ a + b + c = 0
⇒ (2) có nghiệm t 1 = 1 ; t 2 = c / a = 3 .
+ t = 1 ⇒ x + 1/x = 1 ⇔ x 2 + 1 = x ⇔ x 2 – x + 1 = 0
Có a = 1; b = -1; c = 1 ⇒ Δ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
Phương trình vô nghiệm.

Giải các phương trình sau (Đặt ẩn phụ)
d) x(x+1)(x2+x+1)=42
e) (x-1)(x-3)(x+5)(x+7)-297=0
f) x4-2x2-144x-1295=0
d: \(x\left(x+1\right)\left(x^2+x+1\right)=42\left(1\right)\)
=>\(\left(x^2+x\right)\left(x^2+x+1\right)=42\)
Đặt \(a=x^2+x\)
Phương trình (1) sẽ trở thành \(a\left(a+1\right)=42\)
=>\(a^2+a-42=0\)
=>(a+7)(a-6)=0
=>\(\left(x^2+x+7\right)\left(x^2+x-6\right)=0\)
mà \(x^2+x+7=\left(x+\dfrac{1}{2}\right)^2+\dfrac{27}{4}>0\forall x\)
nên \(x^2+x-6=0\)
=>(x+3)(x-2)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
e: \(\left(x-1\right)\left(x-3\right)\left(x+5\right)\left(x+7\right)-297=0\left(2\right)\)
=>\(\left(x-1\right)\left(x+5\right)\left(x-3\right)\left(x+7\right)-297=0\)
=>\(\left(x^2+4x-5\right)\left(x^2+4x-21\right)-297=0\)
Đặt \(b=x^2+4x\)
Phương trình (2) sẽ trở thành \(\left(b-5\right)\left(b-21\right)-297=0\)
=>\(b^2-26b+105-297=0\)
=>\(b^2-26b-192=0\)
=>(b-32)(b+6)=0
=>\(\left(x^2+4x-32\right)\left(x^2+4x+6\right)=0\)
mà \(x^2+4x+6=\left(x+2\right)^2+2>0\forall x\)
nên \(x^2+4x-32=0\)
=>(x+8)(x-4)=0
=>\(\left[{}\begin{matrix}x+8=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=4\end{matrix}\right.\)
f: \(x^4-2x^2-144x-1295=0\)
=>\(x^4-7x^3+7x^3-49x^2+47x^2-329x+185x-1295=0\)
=>\(\left(x-7\right)\cdot\left(x^3+7x^2+47x+185\right)=0\)
=>\(\left(x-7\right)\left(x+5\right)\left(x^2+2x+37\right)=0\)
mà \(x^2+2x+37=\left(x+1\right)^2+36>0\forall x\)
nên (x-7)(x+5)=0
=>\(\left[{}\begin{matrix}x-7=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-5\end{matrix}\right.\)
Giải các phương trình sau bằng cách đặt ẩn số phụ 2 x 2 + x - 2 2 +10 x 2 +5x -16 =0
Đặt m = 2 x 2 +x -2
Ta có: 2 x 2 + x - 2 2 +10 x 2 +5x -16 =0
⇔ 2 x 2 + x - 2 2 +5(2 x 2 +x -2) -6 =0
⇔ m 2 +5m -6 =0
Phương trình m 2 +5m -6 = 0 có hệ số a = 1, b = 5, c = -6 nên có dạng
a + b + c = 0
Suy ra : m 1 =1 , m 2 =-6
m1 =1 ta có: 2 x 2 +x -2 =1 ⇔ 2 x 2 +x -3=0
Phương trình 2 x 2 +x -3 = 0 có hệ số a = 2, b = 1 , c = -3 nên có dạng
a +b+c=0
Suy ra: x 1 =1 , x 2 =-3/2
Với m=-6 ta có: 2 x 2 +x -2 = -6 ⇔ 2 x 2 +x +4 =0
∆ = 1 2 -4.2.4 = 1 -32 = -31 < 0 . Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm : x 1 =1 , x 2 =-32
giải phương trình (đặt ẩn phụ)
(x2+x)2+4(x2+x)-12=0
Đặt \(x^2+x=t\)
\(\Rightarrow t^2+2t-12=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+x=2\\x^2+x=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+x-2=0\\x^2+x+6=0\left(vn\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
-giải phương trình
4(2x+7)-9(x+3)^2=0
- phân tích đa thức thành nhân tử bằng cách đặt ẩn phụ
(x^2+x+1)*(x^2+x+2)-12
(mọi người giải giúp mình vs ạ)
Bài 1 :
Mình nghĩ phải sửa đề ntn :
\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)\right]^2-\left[3\left(x+3\right)\right]^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)-3\left(x+3\right)\right]\left[2\left(2x+7\right)+3\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(4x+14-3x-9\right)\left(4x+14+3x+9\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(7x+23\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\7x+23=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{-23}{7}\end{cases}}}\)
Vậy....
b) \(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt \(q=x^2+x+1\)ta có :
\(A=q\left(q+1\right)-12\)
\(A=q^2+q-12\)
\(A=q^2+4q-3q-12\)
\(A=q\left(q+4\right)-3\left(q+4\right)\)
\(A=\left(q+4\right)\left(q-3\right)\)
Thay \(q=x^2+x+1\)ta có :
\(A=\left(x^2+x+1+4\right)\left(x^2+x+1-3\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+x-2\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+2x-x-2\right)\)
\(A=\left(x^2+x+5\right)\left[x\left(x+2\right)-\left(x+2\right)\right]\)
\(A=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
Cách 2 của câu 2:
Đặt \(x^2+x+2=t\)
Ta có: \(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
\(=t\left(t-1\right)-12=t^2-t-12\)
\(=\left(t-4\right)\left(t+3\right)=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
Giải các phương trình sau bằng phương pháp đặt ẩn phụ: 3 x 2 + x + 1 – x = x 2 + 3
Giải phương trình (đặt ẩn phụ)
(x2 + x )2 + 4(x2 + x )2 - 12 = 0
đặt x^2 +x+2 =t>0 <=> x^2 +x =t-2
<=>(t-2)^2 +4(t-2) -12 =0
<=>(t-2)(t-2+4)-12 =0
<=>t^2-4 -12 =0
<=>t^2 -16 =0 => t =4
x^2 +x =2 <=>(x-1)(x+2) =0
x=1 ; x =-2