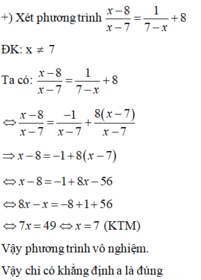Tìm tập nghiệm của phương trình: (x−2)(4x+2)−4x(x+1)=0
HM
Những câu hỏi liên quan
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a) 3x – y = 2; b) x + 5y = 3;
c) 4x – 3y = -1; d) x + 5y = 0 ;
e) 4x + 0y = -2 ; f) 0x + 2y = 5.
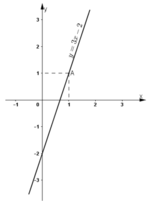
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
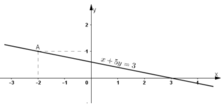
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
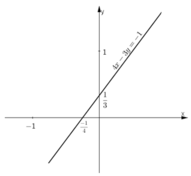
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 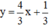
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
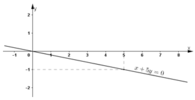
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ 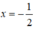
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
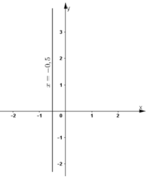
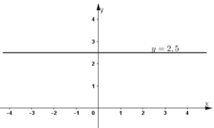
f) 0x + 2y = 5
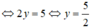
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
Đúng 0
Bình luận (0)
Tìm tập nghiệm của bất phương trình \(\left|x^2-4x\right|\)<0
Do \(\left|x^2-4x\right|\ge0;\forall x\) nên BPT đã cho vô nghiệm
Hay tập nghiệm là \(S=\varnothing\)
Đúng 2
Bình luận (0)
Các khẳng định sau đây đúng hay sai:a. Phương trình
4
x
-
8
+
4
-
2
x
x
2
+
1
0
có nghiệm x 2.b. Phương trình ...
Đọc tiếp
Các khẳng định sau đây đúng hay sai:
a. Phương trình 4 x - 8 + 4 - 2 x x 2 + 1 = 0 có nghiệm x = 2.
b. Phương trình x + 2 2 x - 1 - x - 2 x 2 - x + 1 = 0 có tập nghiệm S = {-2; 1}
c. Phương trình x 2 + 2 x + 1 x + 1 = 0 có nghiệm x = - 1
d. Phương trình x 2 x - 3 x = 0 có tập nghiệm S = {0; 3}
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 
Đúng 0
Bình luận (0)
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình
x
2
+
3
x
x
0
là {0; 3}b) Tập nghiệm của phương trình
x
2
-
4
x
-
2...
Đọc tiếp
Trong các khẳng định sau, số khẳng định đúng là:
a) Tập nghiệm của phương trình x 2 + 3 x x = 0 là {0; 3}
b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0 là {-2}
c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8 là {0}
A. 1
B. 2
C. 0
D. 3
tìm nghiệm
a)\(\sqrt{5x-1}\)=8
b)tập nghiệm của bất phương trình\(\sqrt{5x-2}\)<4
c)\(\sqrt{x-2x+1}-\sqrt{x^2-4x+4}=x-3\)
\(a,ĐK:x\ge\dfrac{1}{5}\\ PT\Leftrightarrow5x-1=64\\ \Leftrightarrow x=13\left(tm\right)\\ b,ĐK:x\ge\dfrac{2}{5}\\ BPT\Leftrightarrow5x-2< 16\\ \Leftrightarrow x< \dfrac{18}{5}\\ \Leftrightarrow\dfrac{2}{5}\le x< \dfrac{18}{5}\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\left|x-1\right|-\left|x-2\right|=x-3\\ \Leftrightarrow\left[{}\begin{matrix}1-x-\left(2-x\right)=x-3\left(x< 1\right)\\x-1-\left(2-x\right)=x-3\left(1\le x< 2\right)\\x-1-\left(x-2\right)=x-3\left(x\ge2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=0\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
tìm m để 1 nghiệm của phương trình 2x^2 - 13x + 2m = 0 gấp dôi 1 nghiệm của pt x^2 - 4x + m = 0
Câu 1: Tìm tất cả các giá trị cuả tham số m để phương trình 4sqrt{x^2-4x+5} x^2-4x+2m-1 có 4 nghiệm phân biệt
Câu 2: Tìm các giá trị của tham số m sao cho tổng các bình phương hai nghiệm của phương trình (m-3)x^2+2x-40 bằng 4
Câu 3: Cho tam giác ABC có BCa, ACb, ABc và I là tâm đường tròn nội tiếp tam giác. Chứng minh rằng: aoverrightarrow{IA}+boverrightarrow{IB}+coverrightarrow{IC}overrightarrow{0}
Câu 4: Cho tam giác ABC. Gọi D,I lần lượt là các điểm xác định bởi 3overrightarrow{BD}-overri...
Đọc tiếp
Câu 1: Tìm tất cả các giá trị cuả tham số m để phương trình \(4\sqrt{x^2-4x+5} =x^2-4x+2m-1\) có 4 nghiệm phân biệt
Câu 2: Tìm các giá trị của tham số m sao cho tổng các bình phương hai nghiệm của phương trình \((m-3)x^2+2x-4=0\) bằng 4
Câu 3: Cho tam giác ABC có \(BC=a, AC=b, AB=c\) và I là tâm đường tròn nội tiếp tam giác. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\)
Câu 4: Cho tam giác ABC. Gọi D,I lần lượt là các điểm xác định bởi \(3\overrightarrow{BD}-\overrightarrow{BC}=\overrightarrow{0}\) và \(\overrightarrow{IA}+\overrightarrow{ID}=\overrightarrow{0}\). Gọi M là điểm thỏa mãn \(\overrightarrow{AM}=x\overrightarrow{AC}\) (x∈R)
a) Biểu thị \(\overrightarrow{BI}\) theo \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\)
b) Tìm x để ba điểm B,I,M thẳng hàng
1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
Đúng 0
Bình luận (0)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
3.
Nối AI kéo dài cắt BC tại D thì D là chân đường vuông góc của đỉnh A trên BC
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{c}{b}\)
\(\Rightarrow\overrightarrow{BD}=\dfrac{c}{b}\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{ID}-\overrightarrow{IB}=\dfrac{c}{b}\left(\overrightarrow{IC}-\overrightarrow{ID}\right)\)
\(\Leftrightarrow b.\overrightarrow{IB}+\overrightarrow{c}.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}\) (1)
Mặt khác:
\(\dfrac{ID}{IA}=\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{a}{b+c}\)
\(\Leftrightarrow\left(b+c\right)\overrightarrow{ID}=-a.\overrightarrow{IA}\) (2)
(1); (2) \(\Rightarrow a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}-\left(b+c\right)\overrightarrow{ID}=\overrightarrow{0}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm tổng bình phương các nghiệm của phương trình \(\left(x-1\right)\left(x-3\right)+3\sqrt{x^2-4x+5}-2=0\)
\(\Leftrightarrow x^2-4x+5+3\sqrt{x^2-4x+5}-2=0\)
Đặt \(\sqrt{x^2-4x+5}=t>0\)
\(\Rightarrow t^2+3t-2=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-3+\sqrt{17}}{2}\\t=\dfrac{-3-\sqrt{17}}{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x^2-4x+5=\dfrac{13-3\sqrt{17}}{2}\)
\(\Leftrightarrow x^2-4x+\dfrac{-3+3\sqrt{17}}{2}=0\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4^2-2\left(\dfrac{-3+3\sqrt{17}}{2}\right)=19-3\sqrt{17}\)
Đúng 1
Bình luận (1)
tìm các giá trị của p để : a) phương trình (p + 1)x - (x+2) =0 vô nghiệm ; b) phương trình p^2 x - p= 4x - 2 có vô số nghiệm
a: \(\Leftrightarrow px-2=0\)
Để phương trình vô nghiệm thì p=0
b: \(\Leftrightarrow x\left(p^2-4\right)=p-2\)
Để phương trình có vô số nghiệm thì p-2=0
hay p=2
Đúng 0
Bình luận (0)