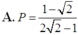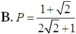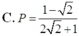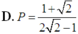Cho a,b là các số dương thỏa mãn a+(1/b)<=1.Tìm gtnn của a/b+(b/a)
Các Ctv hoặc các giáo viên helpp ạ
Cho a,b,c là số thực dương không âm thỏa mãn
Cho a,b,c là số thực dương không âm thỏa mãn \(a+b+c=1\) . Chứng minh rằng :
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}>10\)
Câu 1: Cho a,b là các số dương thỏa mãn a+b=2016. Tìm giá trị lớn nhất của biểu thức P=ab
a.10082 b,2016 c.20162 d.4.20162
Câu 2: Cho a,b là các số dương thỏa mãn ab=16 và đặt P=\(\dfrac{a+b}{2}\). Khẳng định nào sau đây là đúng
a.P≥4 b.P≥8 c.\(\dfrac{17}{2}\) d.5
Câu 3: Cho a, b là các số dương. Tìm giá trị nhỏ nhất của biểu thức P=\(\dfrac{a}{b}+\dfrac{b}{a}\)
a.2 b.0 c.1 d.-2
Câu 4: Tìm mệnh đề đúng
a. a2-a+1>0,∀a b. a2+2a+1>0,∀a c.a2-a≥0, ∀a d.a2-2a-1≥0,∀a
giúp em với ạ
c1:áp dụng bđt AM-GM:
\(a+b\ge2\sqrt{ab}\Rightarrow ab\le\left(\dfrac{a+b}{2}\right)^2=1008^2\)
=> đáp án A
c2: tương tự c1 . đáp án b
3.
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ab}}=2\)
Đáp án A
4.
\(a^2-a+1=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) ;\(\forall a\)
Đáp án A
bài1: Cho a,b,c là các số dương thỏa mãn a+b+c=1
CMR:\(b+c\ge16abc\)
Bài 2: Cho a,b,c là các số dương thỏa mãn a+b+c=1
CMr \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge9\)
Áp dụng BĐT cô si với hai số không âm, Ta có:
\(\left(a+b+c\right)^2=1\ge4a\left(b+c\right)\)
\(\Leftrightarrow b+c\ge4a\left(b+c\right)^2\)
Mà \(\left(b+c\right)^2\ge4bc\forall b,c\ge0\)
\(\Rightarrow b+c\ge16abc\)
Dấu "=" xảy ra khi:
\(\hept{\begin{cases}a+b+c=1\\b=c\\a=b+c\end{cases}}\Rightarrow\hept{\begin{cases}a=\frac{1}{2}\\b=c=\frac{1}{4}\end{cases}}\)
\(\Leftrightarrow\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(\Leftrightarrow3+\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{c}{a}+\frac{a}{c}\right)\ge9\)
\(\Leftrightarrow\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{c}{a}+\frac{a}{c}\right)\ge6\)
Áp dụng BĐT Cô si với 2 số dương ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2,\frac{b}{c}+\frac{c}{b}\ge2,\frac{c}{a}+\frac{a}{c}\ge2\)
\(\Leftrightarrow\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{c}{a}+\frac{a}{c}\right)\ge6\)(đúng)
\(\Leftrightarrow\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge9\)(do a+b+c=1)
cho a b c là các số nguyên dương thỏa mãn c + 1/b = a + b/a chứng minh ab là lập phương của 1 số nguyên dương
Gọi \(d=gcd\left(a;b\right)\) khi đó \(a=dm;b=dn\) với \(\left(m;n\right)=1\)
Ta có:
\(c+\frac{1}{b}=a+\frac{b}{a}\Leftrightarrow c=\frac{b}{a}+a-\frac{1}{b}=\frac{dn}{dm}+dm-\frac{1}{dn}\)
\(=\frac{n}{m}+dm-\frac{1}{dn}=\frac{dn^2+d^2m^2n-m}{dmn}\)
Khi đó \(dn^2+d^2m^2n-m⋮dmn\Rightarrow m⋮n\) mà \(\left(m;n\right)=1\Rightarrow n=1\Rightarrow m=d\)
Khi đó \(ab=dm\cdot dn=d^3\) là lập phương số nguyên dương
cho a,b là các số dương thỏa mãn a+b ≤1
CM: M=ab +1/ab ≥17/4
\(M=ab+\dfrac{1}{16ab}+\dfrac{15}{16ab}\ge2.\sqrt{ab.\dfrac{1}{16ab}}+\dfrac{15}{16.\dfrac{\left(a+b\right)^2}{4}}\ge\dfrac{1}{2}+\dfrac{15}{4}=\dfrac{17}{4}\)
dấu = xảy ra khi x=y=2
tick mik nha
Ta có bất đẳng thức phụ: \(ab\le\dfrac{\left(a+b\right)^2}{4}\le\dfrac{1}{4}\)
Áp dụng bất đẳng thức Cauchy cho 2 số dương:
\(ab+\dfrac{1}{ab}=16ab+\dfrac{1}{ab}-15ab\ge2\sqrt{16ab.\dfrac{1}{ab}}-15.\dfrac{1}{4}=8-\dfrac{15}{4}=\dfrac{17}{4}\)
cho a,b là là các số thực dương thỏa mãn: a+b=1.chứng minh: (a+\(\dfrac{1}{a}\))(b+\(\dfrac{1}{b}\)) ≥ \(\dfrac{25}{4}\)
Áp dụng BĐT cosi:
\(\left(a+\dfrac{1}{a}\right)\left(b+\dfrac{1}{b}\right)4=ab+\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{1}{ab}\\ \ge ab+\dfrac{1}{ab}+2\sqrt{\dfrac{a}{b}\cdot\dfrac{b}{a}}=ab+\dfrac{1}{ab}+2\)
Áp dụng tiếp BĐT cosi:
\(ab+\dfrac{1}{ab}=\left(16ab+\dfrac{1}{ab}\right)-15ab\\ \ge2\sqrt{\dfrac{16ab}{ab}}-15ab=8-15ab\\ \ge8-15\cdot\dfrac{a+b}{4}=8-15\cdot\dfrac{1}{4}=\dfrac{17}{4}\)
\(\Leftrightarrow ab+\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{1}{ab}\ge\dfrac{17}{4}+2=\dfrac{25}{4}\)
Dấu \("="\Leftrightarrow a=b=\dfrac{1}{2}\)
Cho a,b là các số dương thỏa mãn a+b=1 tìm GTNN của P=(1-1/a^2)(1-1/b^2)
Lần sau bạn chú ý viết đề bằng công thức toán
Lời giải:
$P=1-\frac{1}{a^2}-\frac{1}{b^2}+\frac{1}{a^2b^2}$
$=1-\frac{a^2+b^2}{a^2b^2}+\frac{1}{a^2b^2}$
$=1-\frac{(a+b)^2-2ab}{a^2b^2}+\frac{1}{a^2b^2}$
$=1-\frac{1-2ab}{a^2b^2}+\frac{1}{a^2b^2}$
$=1+\frac{2}{ab}$
Áp dụng BĐT Cô-si:
$ab\leq \frac{(a+b)^2}{4}=\frac{1}{4}$
$\Rightarrow \frac{2}{ab}\geq 8$
$\Rightarrow P=1+\frac{2}{ab}\ge 9$
Vậy $P_{\min}=9$ khi $a=b=\frac{1}{2}$
a) Cho a, b, c là ba số nguyên dương nguyên tố cùng nhau thỏa mãn: \(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\) hỏi a + b có là số chính phương không? vì sao?
b) Cho x, y, z là các số dương thỏa mãn: z ≥ 60, x + y + z = 100. Tìm GTLN của A = xyz
Ta có:
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Leftrightarrow\left(a+b\right)c=ab\Leftrightarrow ab-bc-ab=0\)
Hay \(ab-bc-ab+c^2=c^2\Leftrightarrow\left(b-c\right)\left(a-c\right)=c^2\)
Nếu \(\left(b-c;a-c\right)=d\ne1\Rightarrow c^2=d^2\left(loai\right)\)
Vậy \(\left(b-c;a-c\right)=1\Rightarrow c-b;c-a\) là 2 số chính phương
Đặt \(b-c=n^2;a-c=m^2\)
\(\Rightarrow a+b=b-c+a-c+2c=m^2+n^2+2mn=\left(m+n\right)^2\) là số chính phương
cho mình hỏi tại sao ở TH1: c^2=d^2 lại loại vậy ạ
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ b và log a b = 2 . Tính P = log b a a b .
A. P = 1 - 2 2 2 - 1
B. P = 1 + 2 2 2 + 1
C. P = 1 - 2 2 2 + 1
D. P = 1 + 2 2 2 - 1
Đáp án A
Ta có P = 1 2 . 1 - log a b log a b - 1 2 = 1 - 2 2 2 - 1 .
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ b và log a b = 2 . Tính P = log b a a b