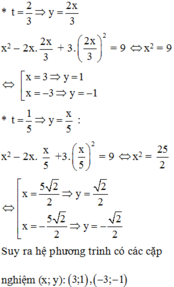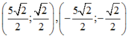tìm nghiệm nguyên của phương trình
x2+3y2+2xy−18(x+y)+73=0x2+3y2+2xy−18(x+y)+73=0
PA
Những câu hỏi liên quan
Giải phương trình: x2+3y2+2xy-18(x+y)=73
\(x^2+3y^2+2xy-18\left(x+y\right)=73\)
\(\Leftrightarrow x^2+3y^2+2xy-18x-18y-73=0\)
\(\Leftrightarrow x^2-2\left(9-y\right)x+3y^2-18y-73=0\)
\(\Delta'=\left(9-y\right)^2-\left(3y^2-18y-73\right)\)
\(=81-18y+y^2-3y^2+18y+73\)
\(=-2y^2+154\)
\(=-2\left(y^2-77\right)\)
Phương trình có nghiệm khi \(\)
\(\Delta'\ge0\Leftrightarrow-2\left(y^2-77\right)\ge0\Leftrightarrow y^2-77\le0\)
\(\Leftrightarrow y^2\le77\Leftrightarrow-\sqrt[]{77}\le y\le\sqrt[]{77}\)
Phương trình có 2 nghiệm là
\(\left[{}\begin{matrix}x_1=9-y+\sqrt[]{-2\left(y^2-77\right)}\\x_2=9-y-\sqrt[]{-2\left(y^2-77\right)}\end{matrix}\right.\) \(\left(-\sqrt[]{77}\le y\le\sqrt[]{77}\right)\)
Đúng 3
Bình luận (0)
tìm nghiệm nguyên của phương trình
\(x^2+3y^2+2xy-18(x+y)+73=0\)
\(\Delta\)không thì dùng cách này cho dễ
\(x^2+3y^2+2xy-18\left(x+y\right)+73=0\)
\(\Leftrightarrow\left(x+y\right)^2-18\left(x+y\right)+81+2y^2=8\)
\(\Leftrightarrow\left(x+y-9\right)^2+2y^2=8\)
\(\Rightarrow2y^2\le8\Rightarrow y^2\le4\Rightarrow-2\le y\le2\)
\(\Rightarrow y\in\left\{\pm1;\pm2;0\right\}\)( do y nguyên )
+) y = 0 \(\Rightarrow\left(x+y-9\right)^2=8\)( loại )
+) y = \(\pm1\)\(\Rightarrow\left(x+y-9\right)^2=6\)( loại )
+) y = \(\pm2\)\(\Rightarrow\left(x+y-9\right)^2=0\Rightarrow x=9-y\Rightarrow\orbr{\begin{cases}x=7\\x=11\end{cases}}\)
Vậy ( x ; y ) \(\in\){ ( 7 ; 2 ) ; ( 11 ; -2 ) }
tìm nghiệm nguyên của phương trình
\(x^2 +3y^2+2xy-18(x+y)+73=0\)
\(\Leftrightarrow\left(x+y\right)^2-18\left(x+y\right)+81=8-2y^2\)
\(\Leftrightarrow\left(x+y-9\right)^2=8-2y^2\le8\)
\(\Rightarrow8-2y^2\) là SCP chẵn không lớn hơn 8
\(\Rightarrow\left[{}\begin{matrix}8-2y^2=0\\8-2y^2=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y^2=4\\y^2=2\left(ktm\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\)
- Với \(y=2\Rightarrow x+y-9=0\Rightarrow x=7\)
- Với \(y=-2\Rightarrow x=9-y=11\)
Cho hệ phương trình
x
2
+
2
x
y
+
8
x
3
y
2
+
12
y...
Đọc tiếp
Cho hệ phương trình x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9 x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0 có nghiệm là (a; b). Khi đó giá trị biểu thức T = 5 a 2 + 4 b 2
A. T = 24
B. T = 21
C. T = 5
D. T = 4
Điều kiện x ≥ − 7 y ≥ − 1 3 *
x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9 ( 1 ) x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0 ( 2 )
Có 1 ⇔ x 2 + 2 y + 4 x − 3 y 2 − 12 y − 9 = 0 , ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được x = − 3 y − 9 x = y + 1
Với x = − 3 y − 9 thì (*) ⇒ − 3 y − 9 ≥ − 7 y ≥ − 1 3 ⇔ y ≤ − 2 3 y ≥ − 1 3 (vô lí)
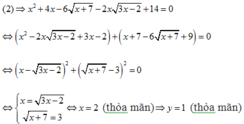
Hệ phương trình có nghiệm là 2 ; 1 ⇒ a = 2 , b = 1 ⇒ T = 24
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Tìm x,y\(\in\)Z thoả mãn đẳng thức: x2-3y2+2xy+2x-4y-7=0
x2 - 3y2 + 2xy + 2x - 4y - 7 = 0
<=> 4.(x2 - 3y2 + 2xy + 2x - 4y - 7) = 0
<=> 4x2 - 12y2 + 8xy + 8x - 16y - 28 = 0
<=> (4x2 + 8xy + 4y2) + (8x + 8y) + 4 - 16y2 - 24y - 32 = 0
<=> (2x + 2y)2 + 4(2x + 2y) + 4 - (16y2 + 24y + 9) = 23
<=> (2x + 2y + 2)2 - (4y + 3)2 = 23
<=> (2x + 6y + 5)(2x - 2y - 1) = 23
Vì \(x;y\inℤ\Rightarrow2x+6y+5;2x-2y-1\inℤ\)
Lập bảng :
| 2x + 6y + 5 | 1 | 23 | -1 | -23 |
| 2x - 2y - 1 | 23 | 1 | -23 | -1 |
| x | 17/2(loại) | 3 | -9 | -7/2(loại) |
| y | 2 | 2 |
Vậy (x;y) = (3;2) ; (-9;2)
Đúng 4
Bình luận (0)
Tìm nghiệm nguyên x, y của pt: \(6x^2+10y^2+2xy-x-28y+18=0\)
\(6x^2+\left(2y-1\right)x+10y^2-28y+18=0\)
\(\Delta=\left(2y-1\right)^2-24\left(10y^2-28y+18\right)\ge0\)
\(\Leftrightarrow-236y^2+668y-431\ge0\)
\(\Rightarrow\dfrac{167-2\sqrt{615}}{118}\le y\le\dfrac{167+2\sqrt{615}}{118}\)
\(\Rightarrow y=1\)
Thế vào pt đầu ...
Đúng 2
Bình luận (0)
Tìm cặp số (x;y) thỏa:
a) x2 + 3y2 - 4x + 6y + 7 = 0.
b) 3x2 y2 + 10x - 2xy + 26 = 0.
c) 3x2 + 6y2 - 12x - 20y + 40 = 0.
a: \(x^2+3y^2-4x+6y+7=0\)
\(\Leftrightarrow x^2-4x+4+3y^2+6y+3=0\)
\(\Leftrightarrow\left(x-2\right)^2+3\left(y+1\right)^2=0\)
\(\Leftrightarrow\left(x,y\right)=\left(-2;1\right)\)
Đúng 0
Bình luận (0)
Hệ phương trình
x
2
-
2
x
y
+
3
y
2
9
2
x...
Đọc tiếp
Hệ phương trình x 2 - 2 x y + 3 y 2 = 9 2 x 2 - 13 x y + 15 y 2 = 0 có nghiệm là?
A. (3; 1); (−3; −1)
B. 5 2 2 ; 2 2 ; - 5 2 2 ; - 2 2
C. (3; 1); (−3; −1); 5 2 2 ; 2 2 ; - 5 2 2 ; - 2 2
D. (3; −1); (−3; 1); 5 2 2 ; 2 2 ; - 5 2 2 ; - 2 2
Bài 4: Cho x, y là hai số thỏa mãn : x + 2y = 3. Tìm giá trị nhỏ nhất của E = x2 + 2y2
Bài 5 : Cho hai số x, y thỏa mãn : x2 + 3y2 + 2xy – 10x – 14y + 18 = 0. Tìm GTLN ; GTNN của biểu thức P = x + y
bài 4 : ta có : \(x+2y=3\Leftrightarrow x=3-2y\)
\(\Rightarrow E=x^2+2y^2=\left(3-2y\right)^2+2y^2=4y^2-12y+9+2y^2\)
\(=6y^2-12y+6+3=6\left(y-1\right)^2+3\ge3\)
\(\Rightarrow E_{max}=3\) khi \(x=y=1\)
bài 5 : ta có : \(x^2+3y^2+2xy-10x-14y+18=0\)
\(\Leftrightarrow2y^2-4y+2=-\left(x^2+2xy+y^2\right)+10\left(x+y\right)-16\)
\(\Leftrightarrow2\left(y-1\right)^2=-\left(x+y\right)^2+10\left(x+y\right)-16\ge0\)
\(\Leftrightarrow2\le x+y\le8\)
\(\Rightarrow P_{min}=2\) khi \(\left\{{}\begin{matrix}y=1\\x+y=2\end{matrix}\right.\Leftrightarrow x=y=1\)
\(\Rightarrow P_{max}=8\) khi \(\left\{{}\begin{matrix}y=1\\x+y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)
vậy ...........................................................................................................................
Đúng 0
Bình luận (0)