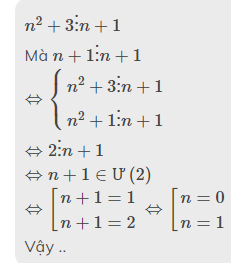Tìm n để:a) n+5 chia hết n+1b) 3n+2 chia hết n-1
LM
Những câu hỏi liên quan
Bài 2: Tìm số tự nhiên n để:
a)(3n+5) chia hết cho n
b) (7n+4) chia hết cho n
c) (27-4n) chia hết cho n ( n<7)
\(a,\Rightarrow n\inƯ\left(5\right)=\left\{1;5\right\}\\ b,\Rightarrow n\inƯ\left(4\right)=\left\{1;2;4\right\}\\ c,\Rightarrow n\inƯ\left(27\right)=\left\{1;3\right\}\left(n< 7\right)\)
Đúng 3
Bình luận (0)
Tìm số nguyên n để:
a) n3 – 2 chia hết cho n – 2
b) n3 – 3n2 – 3n – 1 chia hết cho n2 + n + 1
c) 5n – 2n chia hết cho 63
giúp vs ạ...
a: \(n^3-2⋮n-2\)
=>\(n^3-8+6⋮n-2\)
=>\(6⋮n-2\)
=>\(n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)
b: \(n^3-3n^2-3n-1⋮n^2+n+1\)
=>\(n^3+n^2+n-4n^2-4n-4+3⋮n^2+n+1\)
=>\(3⋮n^2+n+1\)
=>\(n^2+n+1\in\left\{1;-1;3;-3\right\}\)
mà \(n^2+n+1=\left(n+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall n\)
nên \(n^2+n+1\in\left\{1;3\right\}\)
=>\(\left[{}\begin{matrix}n^2+n+1=1\\n^2+n+1=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n^2+n=0\\n^2+n-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}n\left(n+1\right)=0\\\left(n+2\right)\left(n-1\right)=0\end{matrix}\right.\Leftrightarrow n\in\left\{0;-1;-2;1\right\}\)
Đúng 3
Bình luận (0)
Bài 4: Chứng minh rằng:a) 4^{10}+4^7 chia hết cho 65 b) 10^{10}-10^9-10^8 chia hết cho 89Bài 5. Tìm số tự nhiên n để:a) 5n+4 chia hết cho nb) n+6 chia hết cho n+2c) 3n+1 chia hết cho n-2d) 3n+9 chia hết cho 2n-1Bài 6: chứng minh rằng:overline{abab} chia hết cho 101overline{abc-overline{cba}} chia hết cho 9 và 11
Đọc tiếp
Bài 4: Chứng minh rằng:
a) \(4^{10}+4^7\) chia hết cho 65
b) \(10^{10}-10^9-10^8\) chia hết cho 89
Bài 5. Tìm số tự nhiên n để:
a) 5n+4 chia hết cho n
b) n+6 chia hết cho n+2
c) 3n+1 chia hết cho n-2
d) 3n+9 chia hết cho 2n-1
Bài 6: chứng minh rằng:
\(\overline{abab}\) chia hết cho 101
\(\overline{abc-\overline{cba}}\) chia hết cho 9 và 11
Bài 5:
b: Ta có: \(n+6⋮n+2\)
\(\Leftrightarrow n+2\in\left\{2;4\right\}\)
hay \(n\in\left\{0;2\right\}\)
c: Ta có: \(3n+1⋮n-2\)
\(\Leftrightarrow n-2\in\left\{-1;1;7\right\}\)
hay \(n\in\left\{1;3;9\right\}\)
Đúng 0
Bình luận (0)
Tìm số tự nhiên n khác 0 sao cho
a) n+6 chia hết cho n-1
b)3n+5 chia hết cho n+1
\(a,\Rightarrow n-1+7⋮n-1\)
Mà \(n-1⋮n-1\Rightarrow7⋮n-1\)
\(\Rightarrow n-1\inƯ\left(7\right)=\left\{1;7\right\}\\ \Rightarrow n\in\left\{2;8\right\}\)
\(b,\Rightarrow3\left(n+1\right)+2⋮n+1\)
Mà \(3\left(n+1\right)⋮n+1\Rightarrow2⋮n+1\)
\(\Rightarrow n+1\inƯ\left(2\right)=\left\{1;2\right\}\\ \Rightarrow n=1\left(n\ne0\right)\)
Đúng 2
Bình luận (0)
Bài 4: Tìm số tự nhiên n sao cho:
a) 4n - 5 chia hết cho 2n - 1
b) n2 + 3n + 1 chia hết cho n +1
a,
Ta có: 4n-5 chia hết cho 2n-1
=>4n-2-3 chia hết cho 2n-1
=>2.(2n-1)-3 chia hết cho 2n-1
=>3 chia hết cho 2n-1
=>2n-1=Ư(3)=(-1,-3,1,3)
=>2n=(0,-2,2,4)
=>n=(0,-1,1,2)
Vậy n=0,-1,1,2
Đúng 0
Bình luận (0)
tìm n để:a) 28 chia hết cho 2n+1
b)n2+1 thuộc Ư(26)
c)n+3 chia hết cho n+1
d)n2-n+2 chia hết cho n-1
e)2n+5 chia hết cho n+2
Tìm n thuộc Z:
1)n+5 chia hết n
2)3n+2 chia hết n
3)-2n+3 chia hết n
4)5n chia hết n-1
5)4n chia hết 1+n
6)10-3n chia hết 1-n
7)n+5 chia hết 1+n
8)3n-5 chia hết n-1
9) 2n+3 chia hết 2n+1
10) 6n+5 chia hết 3n-2
1 tìm n thuộc z biết
a, 7 chia hết n-2
2 tìm n thuộc z biết
a, 2n+5 chia hết cho n-1
b, n+3 chia hết cho 2n -1
3 tìm n thuộc z biết
a, 2n-5 chia hết cho n+1 và n+1 chia hết cho 2n+5
b, 3n+2 chia hết cho n-2 và n-2 chia hết cho 3n+2
Tìm n thuộc N để:
a, 3n+2 chia hết n-1
b, n^2+1 chia hết 16-3n
c, n^2 +1 chia hết n-1
d, n+8 chia hết n+3
e, n+6 chia hết-1
g, 4n-5 chia hết 2n-1
h,12-n chia hết 8-n
i, 2n+1 chia hết 16-3n
a, 3n+2 chia hết n-1
=> 3(n-1)+5 chia hết cho n-1
Mà 3(n-1) chia hết cho n-1
=> 5 chia hết cho n-1
Lại có n thuộc N
=> n-1 thuộc Ư(5)=1,-1,5,-5
=> n=2,0,6,-4
Đúng 0
Bình luận (0)
dấu gạch trước mấy số là âm hay dấu trừ
Đúng 0
Bình luận (0)
bài 1 : tình ( bằng cách hợp lí nếu có thể )
a ) - - 175 . 16 - 84 . 175
b) ( 16 - 39 ) - ( 158 + 16 - 39 )
Xem thêm câu trả lời