Tìm GTNN của hàm số y=4/x + 9/1-x với 0<x<1
1. Tìm GTNN m của hàm số f(x)= \(\dfrac{4}{x}\) + \(\dfrac{x}{1-x}\) với 1>x>0
2. Tìm GTNN m của hàm số f(x)= \(\dfrac{1}{x}\) + \(\dfrac{1}{1-x}\) với 0<x<1
Giúp mk với nhé thanks trước.
1.
\(f\left(x\right)=\dfrac{4}{x}+\dfrac{x-1+1}{1-x}=\dfrac{2^2}{x}+\dfrac{1}{1-x}-1\ge\dfrac{\left(2+1\right)^2}{x+1-x}-1=8\)
\(f\left(x\right)_{min}=8\) khi \(x=\dfrac{2}{3}\)
2.
\(f\left(x\right)=\dfrac{1}{x}+\dfrac{1}{1-x}\ge\dfrac{4}{x+1-x}=4\)
\(f\left(x\right)_{min}=4\) khi \(x=\dfrac{1}{2}\)
Tìm GTNN (min y) của hàm số y = log 3 x 2 + x + 1 - log 3 x với x > 0.
A. 0
B. 1
C. 1 2
D. 1 3
TÌM GTNN CỦA HÀM SỐ SAU:
a) y=\(\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}\)
TÌM GTLN CỦA HÀM SỐ SAU:
b)y= \(x^2\sqrt{9-x^2}với-3\le x\le3\)
c)y=\(\left(1-x\right)^3\left(1+3x\right)với\dfrac{-1}{3}\le x\le1\)
\(a,\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}=\dfrac{x^2+x+1+1}{\sqrt{x^2+x+1}}=\sqrt{x^2+x+1}+\dfrac{1}{\sqrt{x^2+x+1}}\left(1\right)\)
Áp dụng BĐT cosi: \(\left(1\right)\ge2\sqrt{\sqrt{x^2+x+1}\cdot\dfrac{1}{\sqrt{x^2+x+1}}}=2\)
Dấu \("="\Leftrightarrow x^2+x+1=1\Leftrightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Tìm GTNN của hàm số \(Y=\dfrac{x^2+2x+33}{4x-4}\) với x>1
\(y=\dfrac{x+3}{4}+\dfrac{9}{x-1}=\dfrac{x-1}{4}+\dfrac{9}{x-1}+1\)
\(y\ge2\sqrt{\dfrac{9\left(x-1\right)}{4\left(x-1\right)}}+1=4\)
\(y_{min}=4\) khi \(x=7\)
Cho số thực x thỏa mãn 0 < x < 1. Tìm GTNN của hàm số:
y = 1 x + 1 1 - x
Vì
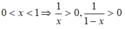
Áp dụng bất đẳng thức Cô – si đối với hai số 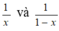 ta được:
ta được:
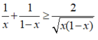
Vì 0 < x < 1 ⇒ 1 - x > 0
Áp dụng bất đẳng thức Cô – si đối với hai số 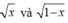 ta được:
ta được:
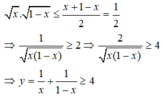
Dấu “ = ” xảy khi và chỉ khi
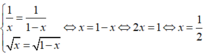
Vậy giá trị nhỏ nhất của hàm số bằng 4 tại x = 1/2
cho hàm số y=(2m-1)x2 (m:tham số)
a,Tìm m dể hàm số đạt GTNN bằng 0 khi x=0
b,Tìm m để hàm số đồng biến khi x<0 và nghịch biến khi x>0
c, Tìm m để đồ thị hàm số đi qua (1;2) và vẽ đồ thị hàm số với m vừa tìm được.
a) Để hàm số đạt giá trị nhỏ nhất bằng 0 khi x=0 thì 2m-1>0
\(\Leftrightarrow2m>1\)
hay \(m>\dfrac{1}{2}\)
b) Để hàm số đồng biến khi x<0 và nghịch biến khi x>0 thì 2m-1<0
\(\Leftrightarrow2m< 1\)
hay \(m< \dfrac{1}{2}\)
Tìm GTNN của hàm số:
y = \(\frac{2}{1-x}+\frac{1}{x}\) với (0<x<1)
Ta có :
\(y=\frac{2}{1-x}+\frac{1}{x}\)
\(\Rightarrow y=\frac{2\left(1-x\right)+2x}{1-x}+\frac{1-x+x}{x}\)
\(\Rightarrow y=2+\frac{2x}{1-x}+\frac{1-x}{x}+1\)
\(\Rightarrow y=\frac{2x}{1-x}+\frac{1-x}{x}+3\)
Vì \(0< x< 1\Rightarrow\hept{\begin{cases}\frac{2x}{1-x}>0\\\frac{1}{x}>0\end{cases}}\)
Áp dụng BĐT Cô si cho 2 số dương , ta có :
\(\Rightarrow y=\frac{2x}{1-x}+\frac{1-x}{x}+3\ge2\sqrt{\frac{2x}{1-x}.\frac{1-x}{x}}+3=2\sqrt{2}+3\)
Dấu "=" xảy ra khi \(\frac{2x}{1-x}=\frac{1-x}{x}\Leftrightarrow\left(1-x\right)^2=2x^2\Leftrightarrow x^2+2x-1=0\Leftrightarrow\left(x+1\right)^2=2\Rightarrow x=\sqrt{2}-1\)
( vì\(0< x< 1\) )
Vậy \(Min_y=2\sqrt{2}+3\) khi \(x=\sqrt{2}-1\)
\(y=\frac{2}{1-x}+\frac{1}{x}\ge\frac{\left(\sqrt{2}+1\right)^2}{1-x+x}=3+2\sqrt{2}\)
Dấu = xảy ra khi
\(\frac{\sqrt{2}}{1-x}=\frac{1}{x}\)
\(\Leftrightarrow x=\frac{1}{1+\sqrt{2}}=\sqrt{2}-1\)
cho hàm số y=(2m-1)x2 (m:tham số)
a,Tìm m dể hàm số đạt GTNN bằng 0 khi x=0
b,Tìm m để hàm số đồng biến khi x<0 và nghịch biến khi x>0
Tìm GTLN-GTNN của hàm số y= \(^{x^4}\)-\(2x^2\) với x thuộc [-2;1]
help me
Đạo hàm đi bạn :D Cho nhanh
\(y=f\left(x\right)=x^4-2x^2\)
\(\Rightarrow f'\left(x\right)=4x^3-4x\)
\(f'\left(x\right)=0\Leftrightarrow4x^3-4x=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=0\end{matrix}\right.\)
\(f\left(1\right)=-1;f\left(-2\right)=8;f\left(-1\right)=-1;f\left(0\right)=0\)
\(\Rightarrow y_{min}=-1;"="\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(y_{max}=8;"="\Leftrightarrow x=-2\)
Đặt \(x^2=t\left(0\le t\le4\right)\)
\(y=f\left(t\right)=t^2-2t\)
\(minf\left(t\right)=min\left\{f\left(0\right);f\left(4\right);f\left(1\right)\right\}=f\left(1\right)=-1\)
\(maxf\left(t\right)=max\left\{f\left(0\right);f\left(4\right);f\left(1\right)\right\}=f\left(4\right)=8\)
\(min=-1\Leftrightarrow x=\pm1\)
\(max=8\Leftrightarrow x=-2\)
tìm gtln gtnn của hàm số
\(y=\sqrt{1+x}+\sqrt{1-x}+\dfrac{x^2}{4}\)
Lời giải:
TXĐ: $[-1;1]$
$y'=\frac{1}{2\sqrt{x+1}}-\frac{1}{2\sqrt{1-x}}+\frac{x}{2}$
$y'=0\Leftrightarrow x=0$
$f(0)=2$;
$f(1)=f(-1)=\sqrt{2}+\frac{1}{4}$
Vậy $f_{\min}=2; f_{\max}=\frac{1}{4}+\sqrt{2}$