Bài 6: Cho đường tròn (O; R) và dây AB, gọi I là trung điểm của dây AB. Trên tia dối của tia BA lấy điểm M. Kẻ hai tiếp tuyến MC, MD với đường tròn, (C,D ≠ (O)) .
a) Chứng minh rằng: Năm điểm O, I, C, M, D cùng nằm trên một đường tròn.
b) Gọi N là giao điểm của tia OM với (O). Chứng minh rằng N là tâm đường tròn nội tiếp .
ND
Những câu hỏi liên quan
Bài 1: Cho đường tròn (O;3) và điểm M,N sao cho OM=2 căn 2 và ON=3. Xác định vị trí của điểm M và N với (O).
Bài 2:Cho đường tròn (O) và a nằm trên đường tròn. vẽ góc xAy=90độ và Ax, Ay cắt đường tròn tại B và C, biết AB=6, AC=8. tính bán kính đường tròn (O)
Bài 1:
Điểm M nằm trong (O)
Điểm N nằm trên (O)
Đúng 0
Bình luận (0)
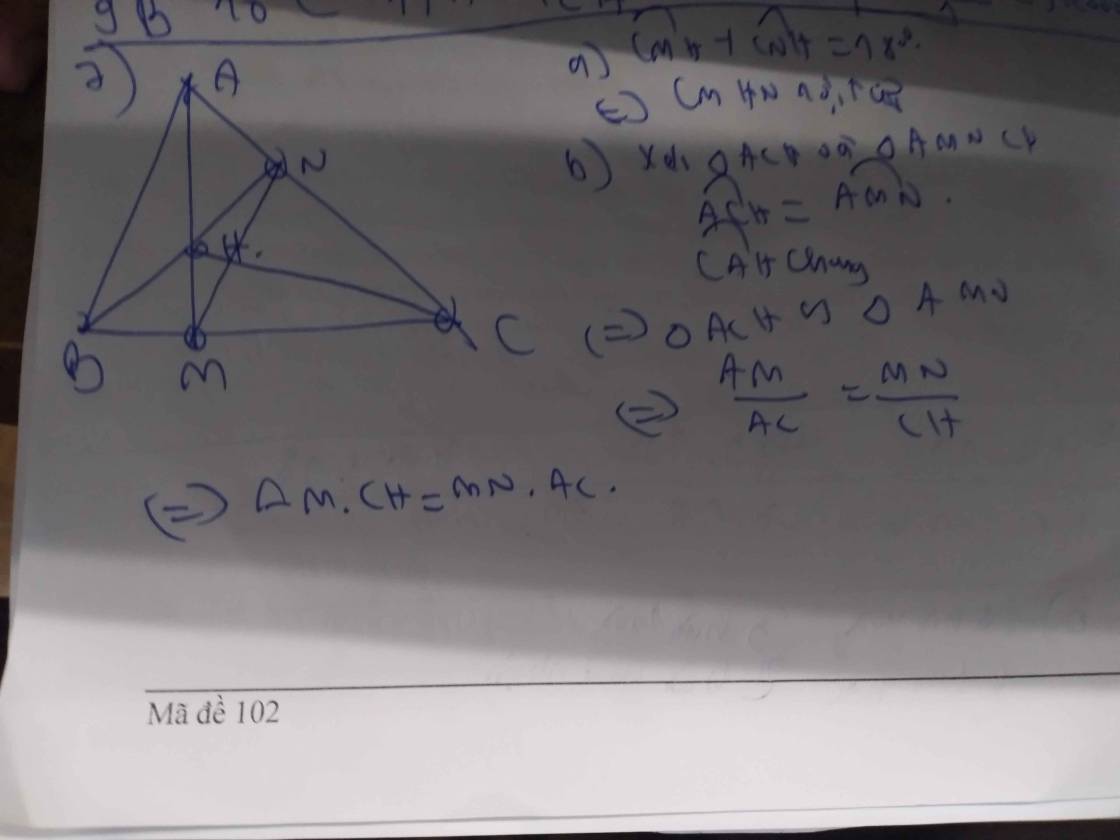
Bài 5:Cho tam giác ABC vuông tại A, có AB 8 cm; AC 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.a)Tính độ dài đoạn BC và AMb)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.c) Chứng minh tứ giác OACE nội tiếp Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (MBC, NAC). Hai đường cao AM và BN cắt nhau tại H.a)Chứng minh rằng tứ giác CMHN nội tiếp một đường trònb)Chứng minh rằng AM.CH AC.MN
Đọc tiếp
Bài 5:Cho tam giác ABC vuông tại A, có AB = 8 cm; AC = 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.
a)Tính độ dài đoạn BC và AM
b)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.
c) Chứng minh tứ giác OACE nội tiếp
Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (M=BC, N=AC). Hai đường cao AM và BN cắt nhau tại H.
a)Chứng minh rằng tứ giác CMHN nội tiếp một đường tròn
b)Chứng minh rằng AM.CH = AC.MN
Bài 6. (2đ) Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn (O) sao cho OM 2R.Vẽ hai tiếp tuyến MA và MB (A, B là tiếp điểm) đến (O). Gọi H là giao điểm của AB và OM.Kẻ đường kính AC của (O).a. Chứng minh: OM⏊AB và BC//OM.b. Tia CH cắt đường tròn (O) tại K (K khác C) và tia AK cắt đoạn OM tại I. Chứng minhHO.HM AK.AI và ∆AHI đồng dạng ∆CBH.c. Chứng minh I là trung điểm HM.
Đọc tiếp
Bài 6. (2đ) Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn (O) sao cho OM > 2R.
Vẽ hai tiếp tuyến MA và MB (A, B là tiếp điểm) đến (O). Gọi H là giao điểm của AB và OM.
Kẻ đường kính AC của (O).
a. Chứng minh: OM⏊AB và BC//OM.
b. Tia CH cắt đường tròn (O) tại K (K khác C) và tia AK cắt đoạn OM tại I. Chứng minh
HO.HM = AK.AI và ∆AHI đồng dạng ∆CBH.
c. Chứng minh I là trung điểm HM.
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
TỪ (1) và (2) suy ra OM⊥AB
Đúng 1
Bình luận (0)
Bài 1 : Cho đường tròn ( O ; R ) đường kính AB 5 cm và C là một điểm thuộc đường tròn sao cho AC 3 cm. a) Tam giác ABC là tam giác j? Vì sao? Tính R & Sin góc CAB b) Đường thẳng qua C vuông gó với AB tại H, cắt đường tròn ( O ) tại D. Tính CD & chứng minhrawngf AB là tiếp tuyến của đương tròn (C ; CH )Bài 2 : Cho đường tròn tâm I, bán kính IA a cm, điểm M nằm bên ngoài đườn tròn và cách I là 7 cm, đường thảng đi qua M & tiếp xúc với đường tròn tại B. Tính MBBài 3 : Cho đường tròn tâm O,...
Đọc tiếp
Bài 1 : Cho đường tròn ( O ; R ) đường kính AB = 5 cm và C là một điểm thuộc đường tròn sao cho AC = 3 cm.
a) Tam giác ABC là tam giác j? Vì sao? Tính R & Sin góc CAB
b) Đường thẳng qua C vuông gó với AB tại H, cắt đường tròn ( O ) tại D. Tính CD & chứng minhrawngf AB là tiếp tuyến của đương tròn (C ; CH )
Bài 2 : Cho đường tròn tâm I, bán kính IA = a cm, điểm M nằm bên ngoài đườn tròn và cách I là 7 cm, đường thảng đi qua M & tiếp xúc với đường tròn tại B. Tính MB
Bài 3 : Cho đường tròn tâm O, bán kính 6 cm, một điểm A cách O một khoảng là 10 cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính AB
Bài 6: (3 điểm). Cho đường tròn (O) có đường kính AB và một điểm C thuộc đường tròn (C khác A và B, AC BC). Kẻ OH vuông góc với AC tại H, tia OH cắt tiếp tuyến tai A của đường tròn (0) ở D.a) Chúng minh: DC là tiếp tuyến của (O). b) BD cắt đường tròn (O) tại E (E khác B). Chứng minh: DC2 DB. DEc) Tiếp tuyến tại B của đường tròn (0) cắt đường thẳng CD tại M. Đường thẳng qua C vuông góc với AB cắt BD tại 1. Chứng minh: Ba điểm A, I, M thẳng hàng.
Đọc tiếp
Bài 6: (3 điểm). Cho đường tròn (O) có đường kính AB và một điểm C thuộc đường tròn (C khác A và B, AC > BC). Kẻ OH vuông góc với AC tại H, tia OH cắt tiếp tuyến tai A của đường tròn (0) ở D.
a) Chúng minh: DC là tiếp tuyến của (O).
b) BD cắt đường tròn (O) tại E (E khác B). Chứng minh: DC2 = DB. DE
c) Tiếp tuyến tại B của đường tròn (0) cắt đường thẳng CD tại M. Đường thẳng qua C vuông góc với AB cắt BD tại 1. Chứng minh: Ba điểm A, I, M thẳng hàng.
a: ΔOAC cân tại O
mà OD là đường cao
nên OD là phân giác của góc AOC
Xét ΔOAD và ΔOCD có
OA=OC
góc AOD=góc COD
OD chung
Do đó: ΔOAD=ΔOCD
=>góc OCD=90 độ
=>DC là tiếp tuyến của (O)
b: Xét ΔDCE và ΔDBC có
góc DCE=góc DBC
góc CDE chung
Do đó: ΔDCE đồng dạng với ΔDBC
=>DC/DB=DE/DC
=>DC^2=DB*DE
Đúng 0
Bình luận (0)
Bài 1. Cho đường tròn (O), dây cung CD. Qua O vẽ OH ^ CD tại H, cắt tiếp tuyến tại C của đường tròn (O) tại M. Chứng minh MD là tiếp tuyến của (O).Bài 2. Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tia Ax ^ AB và By ^ AB ở cùng phía nửa đường tròn. Gọi I là một điểm trên nửa đường tròn. Tiếp tuyến tại I cắt Ax tại C và By tại D. Chứng minh rằng AC + BD CD.
Đọc tiếp
Bài 1. Cho đường tròn (O), dây cung CD. Qua O vẽ OH ^ CD tại H, cắt tiếp tuyến tại C của đường tròn (O) tại M. Chứng minh MD là tiếp tuyến của (O).
Bài 2. Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tia Ax ^ AB và By ^ AB ở cùng phía nửa đường tròn. Gọi I là một điểm trên nửa đường tròn. Tiếp tuyến tại I cắt Ax tại C và By tại D. Chứng minh rằng AC + BD = CD.
Bài 6: (2,5 điểm) Từ điểm A ở ngoài đường tròn (O; R) kẻ tiếp tuyến AB (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). Đoạn AC cắt đường tròn (O) tại điểm D (khác C). a) Chứng minh tam giác BDC vuông và . AC A * B ^ 2 A * O ^ 2 - R ^ 2
b) Qua B kẻ đường thẳng d vuông góc với AO tại H. Đường thẳng d cắt đường tròn (O) tại E (khác B). Gọi F là điểm đối xứng của H qua O. Chứng minh tứ giác CEHF là hình chữ nhật và AE là tiếp tuyến của đường tròn (O; R)
c) Tia CH cắt đường tròn (O) tại G....
Đọc tiếp
Bài 6: (2,5 điểm) Từ điểm A ở ngoài đường tròn (O; R) kẻ tiếp tuyến AB (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). Đoạn AC cắt đường tròn (O) tại điểm D (khác C). a) Chứng minh tam giác BDC vuông và . AC = A * B ^ 2 = A * O ^ 2 - R ^ 2 b) Qua B kẻ đường thẳng d vuông góc với AO tại H. Đường thẳng d cắt đường tròn (O) tại E (khác B). Gọi F là điểm đối xứng của H qua O. Chứng minh tứ giác CEHF là hình chữ nhật và AE là tiếp tuyến của đường tròn (O; R) c) Tia CH cắt đường tròn (O) tại G. Chứng minh HA .HO=HG.HC. Suy ra góc GAB bằng góc EAD
a:
Sửa đề: \(AD\cdot AC=AB^2=AO^2-R^2\)
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)CA tại D
Xét ΔBCA vuông tại B có BD là đường cao
nên \(AD\cdot AC=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có \(OB^2+BA^2=OA^2\)
=>\(BA^2+R^2=OA^2\)
=>\(BA^2=OA^2-R^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AC=AB^2=OA^2-R^2\)
b: ΔOBE cân tại O
mà OH là đường cao
nên H là trung điểm của BE
Xét ΔBCE có
O,H lần lượt là trung điểm của BC,BE
=>OH là đường trung bình của ΔBCE
=>OH//CE và OH=1/2CE
OH//CE
F\(\in\)OH
Do đó: HF//CE
\(OH=\dfrac{1}{2}CE\)
\(OH=\dfrac{1}{2}FH\)
Do đó: CE=FH
Xét tứ giác CEHF có
CE//HF
CE=HF
Do đó: CEHF là hình bình hành
Hình bình hành CEHF có \(\widehat{FHE}=90^0\)
nên CEHF là hình chữ nhật
ΔOBE cân tại O
mà OH là đường cao
nên OH là phân giác của góc BOE
Xét ΔOBA và ΔOEA có
OB=OE
\(\widehat{BOA}=\widehat{EOA}\)
OA chung
Do đó: ΔOBA=ΔOEA
=>\(\widehat{OBA}=\widehat{OEA}=90^0\)
=>AE là tiếp tuyến của (O)
c: Xét (O) có
ΔBGC nội tiếp
BC là đường kính
Do đó: ΔBGC vuông tại G
=>GB\(\perp\)GC tại G
Xét ΔHEC vuông tại E và ΔHGB vuông tại G có
\(\widehat{EHC}=\widehat{GHB}\)
Do đó: ΔHEC đồng dạng với ΔHGB
=>\(\dfrac{HE}{HG}=\dfrac{HC}{HB}\)
=>\(HE\cdot HB=HG\cdot HC\)
=>\(HG\cdot HC=HB^2\left(3\right)\)
Xét ΔBOA vuông tại B có BH là đường cao
nên \(HO\cdot HA=HB^2\left(4\right)\)
Từ (3) và (4) suy ra \(HG\cdot HC=HO\cdot HA\)
Đúng 1
Bình luận (0)
Bài 1: Cho một đường tròn (O) dây AB 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.Bài 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PA PB.Bài 3: Cho đường tròn (O;5) và một dây cung AV dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung AB tại M. Tính độ dài dây cung MA.Bài 4: Cho đường tròn (O) và một điểm P bên trong đường tròn. Cmr trong tất cả dây đi qua P thì dây vuông góc...
Đọc tiếp
Bài 1: Cho một đường tròn (O) dây AB = 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.
Bài 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PA = PB.
Bài 3: Cho đường tròn (O;5) và một dây cung AV dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung AB tại M. Tính độ dài dây cung MA.
Bài 4: Cho đường tròn (O) và một điểm P bên trong đường tròn. Cmr trong tất cả dây đi qua P thì dây vuông góc với OP tại P là dây cung ngắn nhất.
Bài 3. Cho nửa đường tròn (O), đường kính AB = 2R. Vẽ đường tròn tâm K đường kính OB.
a) Chứng tỏ hai đường tròn (O) và (K) tiếp xúc nhau.
b) Vẽ dây BD của đường tròn (O) ( BD khác đường kính), dây BD cắt đường tròn (K) tại M.Chứng minh: KM // OD