giải giúp câu 2 tự luận với ạ cảm ơn nhìu
DD
Những câu hỏi liên quan
GIÚP MIK BÀI 1 TỰ LUẬN VỚI Ạ MIK CẢM ƠN NHÌU Ạ
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(BH^2=HA\cdot HC\)
\(\Leftrightarrow BH^2=2\cdot6=12\)
hay \(BH=2\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBHA vuông tại H, ta được:
\(BA^2=BH^2+HA^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{3}\right)^2+2^2=12+4=16\)
hay BA=4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow BC^2=8^2-4^2=48\)
hay \(BC=4\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{CA}=\dfrac{4\sqrt{3}}{8}=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{A}=\dfrac{BA}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
c) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{\sqrt{3}}{2}\)
nên \(\widehat{A}=60^0\)
\(\Leftrightarrow\widehat{C}=30^0\)
Đúng 0
Bình luận (0)
Mong mn giúp em chỉ sửa các đáp án của em, dạ có vài câu em không biết làm mong mn chỉ giúp em ạ
Phần tự luận nhờ mn giả giúp em câu 4 ạ em không biết làm câu đấy ạ
DẠ EM CẢM ƠN MN NHÌU Ạ!

II. Phần tự luận
Câu 1: Động năng của một vật phụu thuộc vào khối lượng và vận tốc
Ví dụ về vật vừa có động năng vừa có thế năng: một chiếc lá đang rơi từ trên cây xuống
Câu 2: Vì nếu cho đá vào trước thì đường và chanh sẽ chậm hòa tan vàotrong nước do nhiệt độ càn cao thì các hạt nguyên tử phân tử chuyển động càng nhanh nên cần hòa tan đường và chanh vào trước để được hòa tan vào trong nước hơn rồi mới nên cho đá vào
Đúng 1
Bình luận (0)
II. Phần tự luận:
Câu 3:
Công thực hiện được:
\(A=F.s=180.8=1440J\)
Công suất của người kéo:
\(\text{℘}=\dfrac{A}{t}=\dfrac{1440}{30}==48W\)
Câu 4:
Đổi: \(12km/h=43,2m/s\)
Công suất của ngựa:
\(\text{℘}=\dfrac{A}{t}=\dfrac{F.s}{t}=F.\dfrac{s}{t}=F.\upsilon=320.43,2=13824W\)
Đúng 2
Bình luận (0)
I. Trắc nghiệm
16.A
17.A
18.D
19.D
20.A
21.B
22.D
23.A
24.B
25.A
26.B
27.C
28.B
Đúng 2
Bình luận (1)
anh chị làm với giải thích ngữ pháp mỗi câu giúp e ạ. e cảm ơn rất nhìu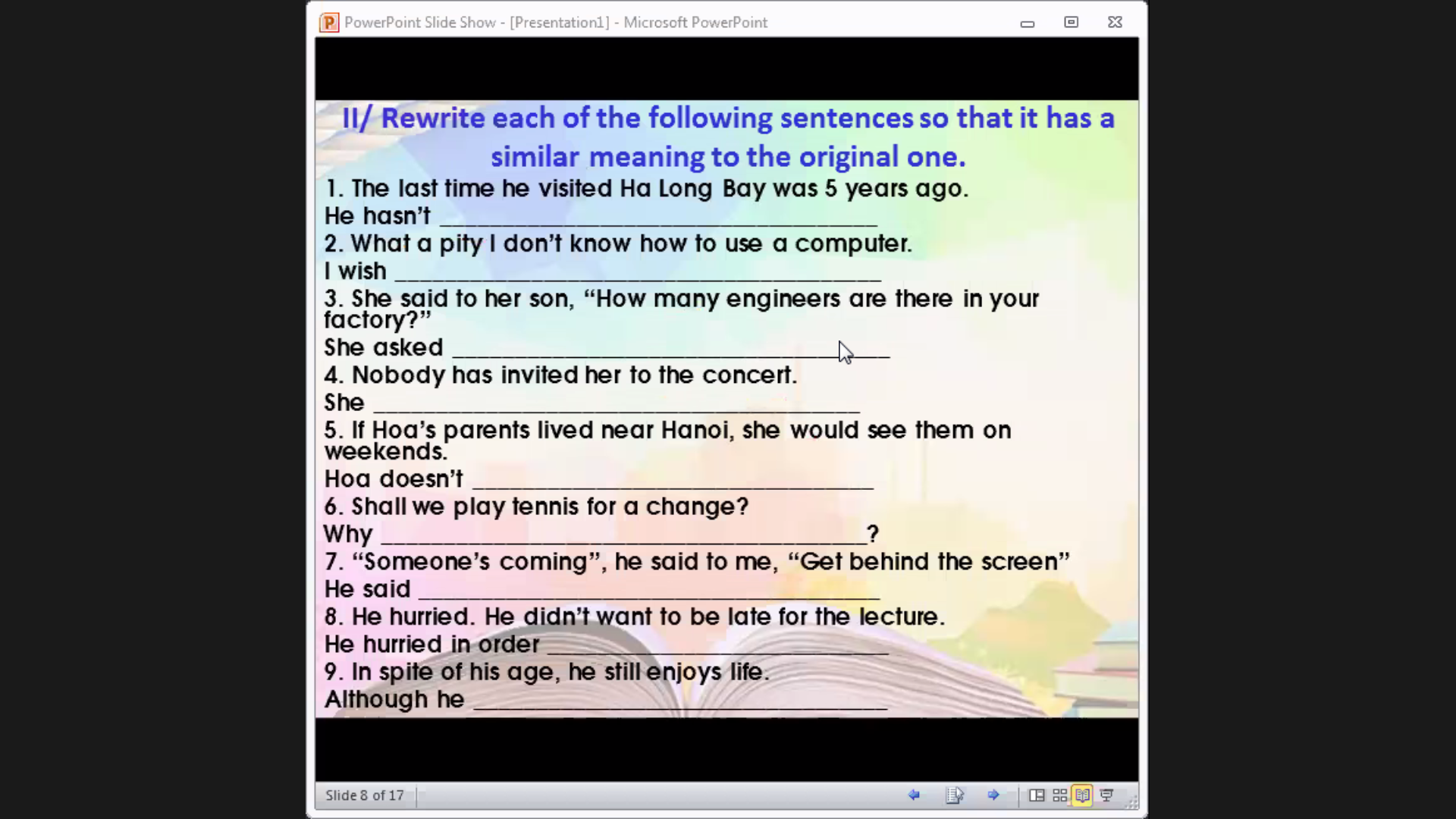
Ai giúp mình giải tự luận bài này với ạ!! Mình cảm ơn nhiều ạ!
Đề bài là: Tính cos2x
Cảm ơn mn nhiều ạ!
Đúng 0
Bình luận (0)
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
\(sin3x.sinx+sin\left(x-\dfrac{\pi}{3}\right)cos\left(x-\dfrac{\pi}{6}\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}cos2x-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin\left(2x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin\left(-\dfrac{\pi}{6}\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}cos2x-\dfrac{1}{2}cos4x-\dfrac{1}{2}cos2x-\dfrac{1}{4}=0\)
\(\Leftrightarrow cos4x+\dfrac{1}{2}=0\)
\(\Leftrightarrow2cos^22x-1+\dfrac{1}{2}=0\)
\(\Leftrightarrow cos^22x=\dfrac{1}{4}\)
\(\Rightarrow cos2x=\pm\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình câu 1,3,4 phần tự luận với ạ. Mình cảm ơn 
1.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow sina< 0\)
\(\Rightarrow sin\alpha=-\sqrt{1-cos^2a}=-\dfrac{12}{13}\)
\(\Rightarrow tan2a=\dfrac{sin2a}{cos2a}=\dfrac{2sina.cosa}{cos^2a-sin^2a}=\dfrac{2.\left(-\dfrac{12}{13}\right).\left(\dfrac{5}{13}\right)}{\left(\dfrac{5}{13}\right)^2-\left(-\dfrac{12}{13}\right)^2}=...\)
3.
\(P=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x}+\dfrac{4}{4y}\ge\dfrac{\left(1+2\right)^2}{x+4y}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(\left(x;y\right)=\left(2;1\right)\)
Đúng 1
Bình luận (0)
4.
Lưu ý: hàm \(sinx\) đồng biến khi \(0< x< 90^0\) và nghịch biến khi \(90^0< x< 180^0\), hàm cos nghịch biến khi \(0< x< 90^0\)
Đường tròn (C) tâm \(I\left(1;1\right)\) bán kính \(R=4\) , \(\overrightarrow{IA}=\left(1;-1\right)\Rightarrow IA=\sqrt{2}\)
Theo công thức diện tích tam giác:
\(S_{IMN}=\dfrac{1}{2}IM.IN.sin\widehat{MIN}=\dfrac{1}{2}R^2.sin\widehat{MIN}=8.sin\widehat{MIN}\)
\(\Rightarrow S_{IMN}\) đạt max khi \(sin\widehat{MIN}\) đạt max
Gọi H là trung điểm MN \(\Rightarrow IH\perp MN\Rightarrow IH\le IA\) theo định lý đường xiên - đường vuông góc
\(\Rightarrow cos\widehat{HIM}=\dfrac{IH}{IM}\le\dfrac{IA}{IM}=\dfrac{\sqrt{2}}{4}\Rightarrow\widehat{HIM}>69^0\)
\(\Rightarrow\widehat{MIN}=2\widehat{HIM}>120^0>90^0\)
\(\Rightarrow sin\widehat{MIN}\) đạt max khi \(\widehat{MIN}\) đạt min
\(\Rightarrow\widehat{HIM}=\dfrac{1}{2}\widehat{MIN}\) đạt min
\(\Rightarrow cos\widehat{HIM}\) đạt max
\(\Rightarrow cos\widehat{HIM}=\dfrac{\sqrt{2}}{4}\Leftrightarrow H\) trùng A
Hay đường thẳng MN vuông góc IA \(\Rightarrow\) MN nhận (1;-1) là 1 vtpt
Phương trình MN: \(1\left(x-2\right)-1\left(y-0\right)=0\Leftrightarrow x-y-2=0\)
Đúng 1
Bình luận (0)
G
Giải giúp em câu tự luận với ạ. Em cảm ơn nhiều
Giải hộ mk câu 2,3,4 tự luận với ạ
Mk cảm ơn nhiều 🤗
Có 6 câu tự luận , ai giúp được câu nào thì giúp em với ạ .. Em cảm ơn 🤧
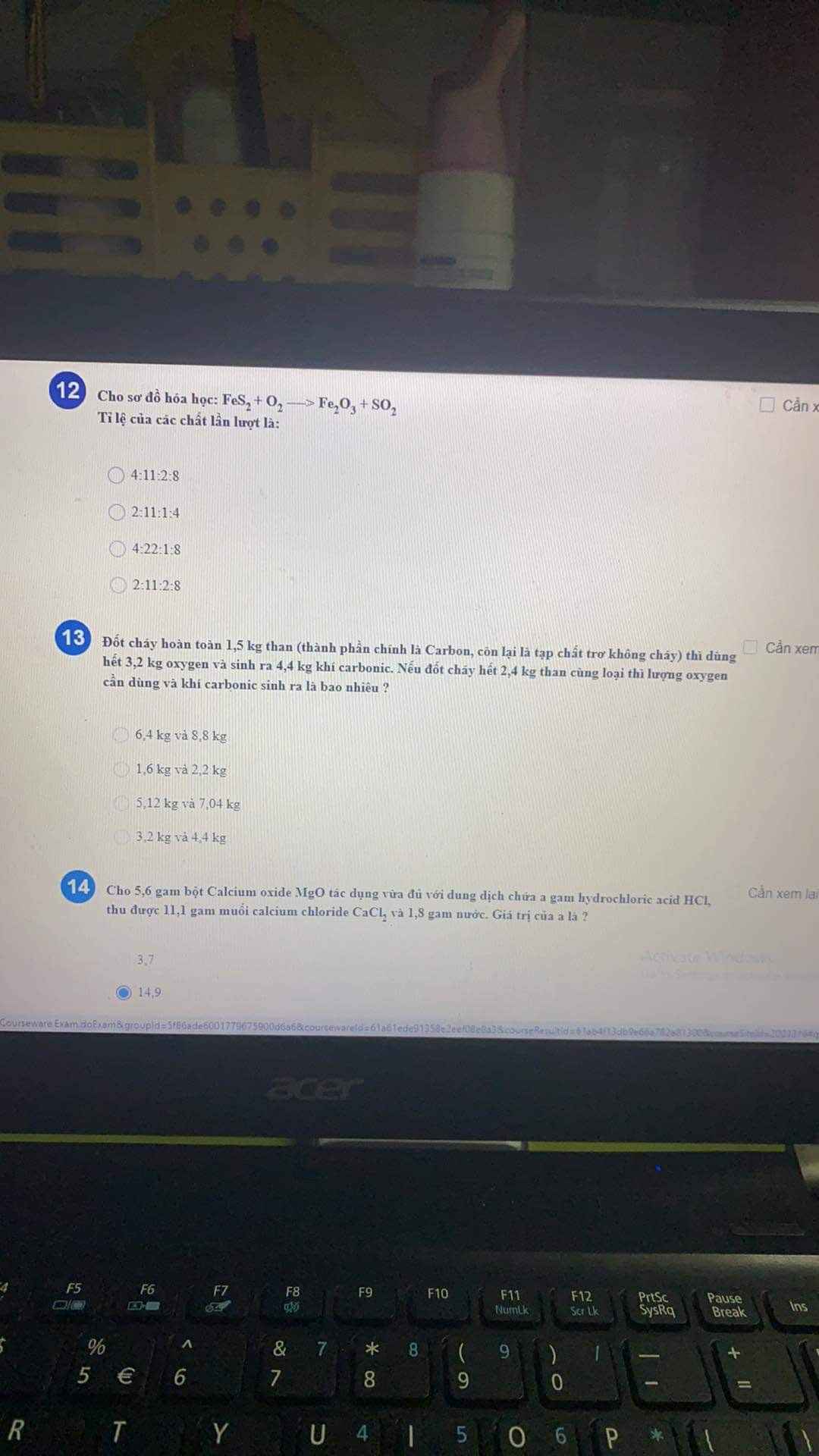
M.n giúp mk câu 13 với ạ, mk cảm ơn rất nhìu(có lời giải chi tiết thì càng tốt nka)



