Cho hai biểu thức E = 5/x-1 và F = 3/x
Tìm các giá trị của x sao cho E + F= E.F
H24
Những câu hỏi liên quan
Cho hàm số yf(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn
∫
0
1
e
x
f
x
d
x
∫
0
1
e
x
f
x
d
x
∫
0
1
e...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn ∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x ≠ 0 . Giá trị của biểu thức e . f ' 1 − f ' 0 e . f 1 − f 0 bằng
A.-2
B.-1
C.2
D.1
Đáp án D
∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x = k ≠ 0
Đặt
u = e x d v = f ' x d x ⇒ d u = e x d x v = f x ⇒ ∫ 0 1 e x f ' x d x = e x f x 0 1 − ∫ 0 1 e x f x d x
⇒ k = e . f 1 − f 0 − k ⇒ e f 1 − f 0 = 2 k .
Đặt
u = e x d v = f ' ' x d x ⇒ d u = e x d x v = f ' x ⇒ ∫ 0 1 e x f ' ' x d x = e x f ' x 0 1 − ∫ 0 1 e x f ' x d x
⇒ k = e . f ' 1 − f ' 0 − k ⇒ e . f ' 1 − f ' 0 = 2 k .
Vậy e . f ' 1 − f ' 0 e . f 1 − f 0 = 2 k 2 k = 1
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn
∫
0
1
e
x
f
x
d
x
∫
0
1
e
x
f
x
d
x
∫
0
1
e
x...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên đoạn [0;1] và thỏa mãn ∫ 0 1 e x f x d x = ∫ 0 1 e x f ' x d x = ∫ 0 1 e x f ' ' x d x ≠ 0 . Giá trị của biểu thức e . f ' 1 − f ' 0 e . f 1 − f 0 bằng
A. -2
B. -1
C. 2
D. 1
a) Cho biểu thức
E
x
+
1
x
2
x
2
+
1
x
2
+...
Đọc tiếp
a) Cho biểu thức E = x + 1 x 2 x 2 + 1 x 2 + 2 x + 1 1 x + 1 .
Chứng minh rằng: Giá trị của biểu thức E luôn bằng 1 với mọi giá trị x ≠ 0 và x ≠ - 1
b) Cho biểu thức F = x + 1 2 x − 2 + 3 x 2 − 1 − x + 3 2 x + 2 . 4 x 2 − 4 5 .
Chứng minh rằng với những giá trị của x hàm F xác định thì giá trị của F không phụ thuộc vào x.
a) Rút gọn E Þ đpcm.
b) Điều kiện xác định E là: x ≠ ± 1
Rút gọn F ta thu được F = 4 Þ đpcm
Đúng 0
Bình luận (0)
câu 1 : số các số nguyên x sao cho biểu thức biểu thức A3/(x+2) nhận giá trị nguyên là ....câu 2 : nếu 0abcdef và (a-b)(c-d)(e-f)x (b-a)(d-c)(f-e) thì x ....câu 3 : A frac{10}{left(x+2right)^2+5}giá trị lớn nhất của biểu thức là ....câu 4 : giá trị nhỏ nhất của biểu thức : A left|x-7right| + 6 -x . Là ....HELP ME
Đọc tiếp
câu 1 : số các số nguyên x sao cho biểu thức biểu thức A=3/(x+2) nhận giá trị nguyên là ....
câu 2 : nếu 0<a<b<c<d<e<f và (a-b)(c-d)(e-f)x= (b-a)(d-c)(f-e) thì x =....
câu 3 : A= \(\frac{10}{\left(x+2\right)^2+5}\)
giá trị lớn nhất của biểu thức là ....
câu 4 : giá trị nhỏ nhất của biểu thức : A = \(\left|x-7\right|\) + 6 -x . Là ....
HELP ME ![]()
Câu 1: Có 4 giá trị
Câu 3: \(A\le\dfrac{10}{5}=2\)
Đúng 0
Bình luận (0)
Cho biểu thức hai biến: f(x; y) = (2x – 3y + 7)(3x + 2y – 1)
a. Tìm các giá trị của y sao cho phương trình (ẩn x) f(x;y) = 0, nhận x = -3 làm nghiệm.
b. Tìm các giá trị của x sao cho phương trình (ẩn y) f(x;y) = 0; nhận y = 2 làm nghiệm.
Bài này có trong sbt toán 8 tập 2 mà!
Đúng 1
Bình luận (7)
a) f(x;y) = 0, nhận x = -3 làm nghiệm
<=> [2. (-3) - 3y + 7][3. (-3) + 2y -1] = 0
\(\Leftrightarrow\left[{}\begin{matrix}-6-3y+7=0\\-9+2y-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-3y=0+6-7=-1\\2y=0+9+1=10\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{3}\\y=5\end{matrix}\right.\)
Vậy:.........
b) f(x;y) = 0; nhận y = 2 làm nghiệm.
\(\Leftrightarrow\left(2x-3.2+7\right)\left(3x+2.2-1\right)=0\)
\(\Leftrightarrow\left(2x-6+7\right)\left(3x+4-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-6+7=0\\3x+4-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0+6-7=-1\\3x=0-4+1=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
Vậy...........
Đúng 1
Bình luận (1)
Cho hàm số f(x) xác định trên R thỏa mãn
f
(
x
)
e
x
+
e
-
x
-
2
, f(0)5 và
f
ln
1
4
0
. Giá trị của biểu thức
S
f
(
-...
Đọc tiếp
Cho hàm số f(x) xác định trên R thỏa mãn f ' ( x ) = e x + e - x - 2 , f(0)=5 và f ln 1 4 = 0 . Giá trị của biểu thức S = f ( - ln 16 ) + f ( ln 4 ) bằng
![]()

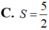
![]()
Cho hàm số f(x) xác định trên R thỏa mãn f (x)
e
x
+
e
-
x
-
2
, f(0)5 và
f
ln
1
4
0
.Giá trị của biểu thức
S
f
-...
Đọc tiếp
Cho hàm số f(x) xác định trên R thỏa mãn f' (x)= e x + e - x - 2 , f(0)=5 và f ln 1 4 = 0 .Giá trị của biểu thức S = f - ln 6 + f ln 4 bằng:
A. S= 31/2.
B. S= 9/2.
C. S= 5/2.
D. S= -7/2
a) 5x/2x+2 +1-6/x+1 b) x2-6/x x+3/2 c) Tìm x sao cho giá trị của biểu thức 3x-2/4 không nhỏ hơn giá trị của biểu thức 3x+3/6d) Tìm x sao cho giá trị của biểu thức (x+1)2 không nhỏ hơn giá trị của biểu thức (x-1)2e) Tìm x sao cho giá trị của biểu thức 2x-3/35 + x(x-2)/7 không lớn hơn giá trị của biểu thức x^2/7-2x-3/5f) Tìm x sao cho giá trị của biểu thức 3x-2/4 không lớn hơn giá trị của biểu thức 3x+3/6
Đọc tiếp
a) 5x/2x+2 +1=-6/x+1
b) x2-6/x = x+3/2
c) Tìm x sao cho giá trị của biểu thức 3x-2/4 không nhỏ hơn giá trị của biểu thức 3x+3/6
d) Tìm x sao cho giá trị của biểu thức (x+1)2 không nhỏ hơn giá trị của biểu thức (x-1)2
e) Tìm x sao cho giá trị của biểu thức 2x-3/35 + x(x-2)/7 không lớn hơn giá trị của biểu thức x^2/7-2x-3/5
f) Tìm x sao cho giá trị của biểu thức 3x-2/4 không lớn hơn giá trị của biểu thức 3x+3/6
Answer:
a) \(\frac{5x}{2x+2}+1=\frac{6}{x+1}\)
\(\Rightarrow\frac{5x}{2\left(x+1\right)}+\frac{2\left(x+1\right)}{2\left(x+1\right)}=\frac{12}{2\left(x+1\right)}\)
\(\Rightarrow5x+2x+2-12=0\)
\(\Rightarrow7x-10=0\)
\(\Rightarrow x=\frac{10}{7}\)
b) \(\frac{x^2-6}{x}=x+\frac{3}{2}\left(ĐK:x\ne0\right)\)
\(\Rightarrow x^2-6=x^2+\frac{3}{2}x\)
\(\Rightarrow\frac{3}{2}x=-6\)
\(\Rightarrow x=-4\)
c) \(\frac{3x-2}{4}\ge\frac{3x+3}{6}\)
\(\Rightarrow\frac{3\left(3x-2\right)-2\left(3x+3\right)}{12}\ge0\)
\(\Rightarrow9x-6-6x-6\ge0\)
\(\Rightarrow3x-12\ge0\)
\(\Rightarrow x\ge4\)
d) \(\left(x+1\right)^2< \left(x-1\right)^2\)
\(\Rightarrow x^2+2x+1< x^2-2x+1\)
\(\Rightarrow4x< 0\)
\(\Rightarrow x< 0\)
e) \(\frac{2x-3}{35}+\frac{x\left(x-2\right)}{7}\le\frac{x^2}{7}-\frac{2x-3}{5}\)
\(\Rightarrow\frac{2x-3+5\left(x^2-2x\right)}{35}\le\frac{5x^2-7\left(2x-3\right)}{35}\)
\(\Rightarrow2x-3+5x^2-10x\le5x^2-14x+21\)
\(\Rightarrow6x\le24\)
\(\Rightarrow x\le4\)
f) \(\frac{3x-2}{4}\le\frac{3x+3}{6}\)
\(\Rightarrow\frac{3\left(3x-2\right)-2\left(3x+3\right)}{12}\le0\)
\(\Rightarrow9x-6-6x-6\le0\)
\(\Rightarrow3x\le12\)
\(\Rightarrow x\le4\)
Cho biểu thức hai biến: \(f\left(x,y\right)=\left(2x-3y+7\right)\left(3x+2y-1\right)\)
a, Tìm các giá trị của y sao cho phương trình ( ẩn x) f(x,y)=0 nhận x=-3 làm nghiệm
b, Tìm các giá trị của x sao cho phương trình ( ẩn y) f(x,y)=0 nhận y=2 làm nghiệm
a, Phương trình f(x,y) =0 <=> (2x-3y+7)(3x+2y-1) =0 nhận x=-3 làm nghiệm nên ta có:(-6-3y +7)(-9 + 2y -1)=0
<=> (1 - 3y)(2y - 10) =0 <=> 1 - 3y=0 hoặc 2y - 10 =0
* 1-3y=0 <=> y=1/3
* 2y - 10= 0 <=> y=5
vậy phương trình nhận x=-3 thì y=1/3 hoặc y=5
b, Phương trình nhận y=2 làm nghiệm nên ta có:
(2x - 6 + 7)(3x+ 4 - 1)=0
<=> (2x + 1)(3x + 3) =0 <=> 2x + 1=0 hoặc 3x + 3 = 0
<=> x=-1/ 2 hoặc x=-1
vậy phương trình nhận y=2 làm nghiệm thì x=-1/2 hoặc x=-1
Đúng 0
Bình luận (0)
a, Phương trình f(x,y) =0 <=> (2x-3y+7)(3x+2y-1) =0 nhận x=-3 làm nghiệm nên ta có:(-6-3y +7)(-9 + 2y -1)=0
<=> (1 - 3y)(2y - 10) =0 <=> 1 - 3y=0 hoặc 2y - 10 =0
* 1-3y=0 <=> y=1/3
* 2y - 10= 0 <=> y=5
vậy phương trình nhận x=-3 thì y=1/3 hoặc y=5
b, Phương trình nhận y=2 làm nghiệm nên ta có:
(2x - 6 + 7)(3x+ 4 - 1)=0
<=> (2x + 1)(3x + 3) =0 <=> 2x + 1=0 hoặc 3x + 3 = 0
<=> x=-1/ 2 hoặc x=-1
vậy phương trình nhận y=2 làm nghiệm thì x=-1/2 hoặc x=-1
Đúng 0
Bình luận (0)