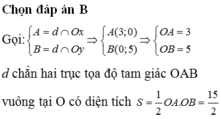Đường thẳng 6x+5y=30 tạo với các trục tọa độ một Tam giác có diện tích bằng bao nhiêu
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
LA
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, đường thẳng tạo với các trục tọa độ một tam giác có diện tích bằng:
A. 15
B. 15 2
C. 3
D. 5
Trong mặt phẳng tọa độ Oxy, đường thẳng d:5x+3y=15 tạo với các trục tọa độ một tam giác có diện tích bằng:
A. 15
B. 15 2
C. 3
D. 5
Bài 8. Cho đường thẳng có phương trình y = (m - 1)x + 2m (m khác 1). Tìm m để đường thẳng cắt hai trục tọa độ và tạo với hai trục tọa độ một tam giác có diện tích bằng 1 (đơn vị diện tích).
Xác định m để đường thẳng y = x + m + 1 tạo với các trục tọa độ một tam giác có diện tích bằng 8 (đvdt)
Gọi giao của đường thẳng và trục Ox là A => A(m+1;0)
=> OA = | m+1 |
Gọi giao của đường thẳng với trục Oy là B => B(0 ; m+1)
=> OB=|m+1|
Theo đề bài ta có S ABC =8
<=> 1/2 x OA x OB= 8
<=> 1/2 x |m+1| x |m+1| = 8
từ đó giải ra m=3
#HT#
Trả lời : m = 3
#HT#
Cho hàm số y 2x-3 có đồ thị là đường thẳng ∆. Đường thẳng ∆ tạo với hai trục tọa độ một tam giác có diện tích bằng: A. 9 B. 9/4 C.9/2 D.3/4
Đọc tiếp
Cho hàm số y= 2x-3 có đồ thị là đường thẳng ∆. Đường thẳng ∆ tạo với hai trục tọa độ một tam giác có diện tích bằng:
A. 9
B. 9/4
C.9/2
D.3/4
+ Giao điểm của đồ thị hàm số y= 2x-3 với trục hoành là điểm A( 3/2; 0).
+ Giao điểm của đồ thị hàm số y= 2x-3 với trục tung là điểm B( 0; -3).
+ Đường thẳng ∆ tạo với hai trục tọa độ ∆ OAB vuông tại O. Suy ra
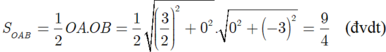
Chọn B.
Đúng 0
Bình luận (0)
xác định m để đường thẳng y:x+m+1 tạo với các trục tọa độ một tam giác có diện tích =8
cho đường thẳng (d): y=(-3x)/4+1/2. viết phương trình đường thẳng (d1) vuông góc với (d) và tạo với hai trục tọa độ một tam giác có diện tích bằng 6 (đơn vị diện tích)
Giúp mik vs
Cho tam giác ABC có: A(-3;2); B(1;1); C(0;-2)
a) Lập phương trình các đường cao, đường trung tuyến, của tam giác ABC
b) Lập phương trình đường thẳng qua M(6;4) và tạo với các trục tọa độ một tam giác có diện tích bằng 2.
Tìm m để đường thẳng d: y=(m2 +2)x+1 tạo với hai trục tọa độ một tam giác có diện tích bằng \(\dfrac{1}{8}\)
Gọi A và B lần lượt là giao điểm của d với Ox và Oy
\(\Rightarrow A\left(-\dfrac{1}{m^2+2};0\right)\) ; \(B\left(0;1\right)\) \(\Rightarrow OA=\dfrac{1}{m^2+2}\) ; \(OB=1\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{8}\Leftrightarrow OA.OB=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{m^2+2}=\dfrac{1}{4}\Rightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
Đúng 0
Bình luận (0)