Cho pt:x2-2mx+4m-4=0.Tìm m để pt có hai nghiệm thỏa mãn (x1+1/x2)+(x2+1)/x1=13/4
NC
Những câu hỏi liên quan
Cho phương trình (ẩn x) : x 2 – 2mx – 4m – 4 = 0(1)
b) Tìm m để phương trình (1) có 2 nghiệm x 1 , x 2 thỏa mãn x 1 2 + x 2 2 - x 1 x 2 = 13 = 13
b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
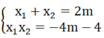
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
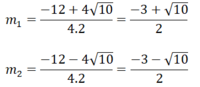
Vậy với 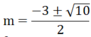 thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
Đúng 0
Bình luận (0)
Cho pt x2 – 2mx -4m -5=0
a) Giải pt khi m= -2
b) Tìm m để pt có 2 nghiệm x1,x2 thỏa mãn ½ x12 - ( m – 1 ) x1+x2 – 2m + 33/2 =4059
a) Thay m=-2 vào phương trình, ta được:
\(x^2+4x+3=0\)
a=1; b=4; c=3
Vì a-b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=-1;x_2=\dfrac{-c}{a}=-3\)
Đúng 0
Bình luận (0)
Cho pt x^2 + 2(m+1)x +4m - 4 =0 a) Tìm m để pt có 2 nghiệm x1, x2 thỏa mãn x1^2 + x2^2 + 3x1.x2 = 0
\(x^2+2\left(m+1\right)+4m-4=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2\left(m+1\right)\\x_1x_2=\dfrac{c}{a}=4m-4\end{matrix}\right.\)
Ta có :
\(x_1^2+x_2^2+3x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+3x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+x_1x_2=0\)
\(\Leftrightarrow\left[-2\left(m+1\right)\right]^2+\left(4m-4\right)=0\)
\(\Leftrightarrow4\left(m^2+2m+1\right)+4m-4=0\)
\(\Leftrightarrow4m^2+8m+4+4m-4=0\)
\(\Leftrightarrow4m^2+12m=0\)
\(\Leftrightarrow4m\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3
cho pt x^2 -2mx+2m-1 =0
1) giải pt với m=1
2) tìm m để pt có 2 nghiệm x1 x2 thoả mãn :a)x1+x2=-1
b)x1^2 +x2^2=13
1) Thay m=1 vào phương trình, ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1
Vậy: Khi m=1 thì phương trình có nghiệm duy nhất là x=1
Đúng 0
Bình luận (0)
1) Bạn tự làm
2) Ta có: \(\Delta'=\left(m-1\right)^2\ge0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m-1\end{matrix}\right.\)
a) Ta có: \(x_1+x_2=-1\) \(\Rightarrow2m=-1\) \(\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy ...
b) Ta có: \(x_1^2+x_2^2=13\) \(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2=13\)
\(\Rightarrow4m^2-4m-11=0\) \(\Leftrightarrow m=\dfrac{1\pm\sqrt{13}}{2}\)
Vậy ...
Đúng 1
Bình luận (1)
2) Ta có: \(\text{Δ}=\left(-2m\right)^2-4\cdot1\cdot\left(2m-1\right)=4m^2-8m+4=\left(2m-2\right)^2\ge0\forall m\)
Do đó, phương trình luôn có nghiệm với mọi m
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m}{1}=-2m\\x_1\cdot x_2=\dfrac{2m-1}{1}=2m-1\end{matrix}\right.\)
a) Ta có: \(x_1+x_2=-1\)
\(\Leftrightarrow-2m=-1\)
hay \(m=\dfrac{1}{2}\)
b) Ta có: \(x_1^2+x_2^2=13\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=13\)
\(\Leftrightarrow\left(-2m\right)^2-2\cdot\left(2m-1\right)=13\)
\(\Leftrightarrow4m^2-4m+2-13=0\)
\(\Leftrightarrow4m^2-4m+1-12=0\)
\(\Leftrightarrow\left(2m-1\right)^2=12\)
\(\Leftrightarrow\left[{}\begin{matrix}2m-1=2\sqrt{3}\\2m-1=-2\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\sqrt{3}+1\\2m=-2\sqrt{3}+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{2\sqrt{3}+1}{2}\\m=\dfrac{-2\sqrt{3}+1}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho pt : x^2 - 2mx + m^2 - m = 0 (1) ( m là tham số ). Tìm các giá trị của tham số m để pt (1) có 2 nghiệm phân biệt x1,x2 thỏa mãn x1^2 + x2^2 = 4 - 3x1x2
Δ=(-2m)^2-4(m^2-m)
=4m^2-4m^2+4m=4m
Để (1) có 2 nghiệm phân biệt thì 4m>0
=>m>0
x1^2+x2^2=4-3x1x2
=>(x1+x2)^2-2x1x2=4-3x1x2
=>(2m)^2+m^2-m=4
=>4m^2+m^2-m-4=0
=>5m^2-m-4=0
=>5m^2-5m+4m-4=0
=>(m-1)(5m+4)=0
=>m=1 hoặc m=-4/5(loại)
Đúng 1
Bình luận (0)
cho phương trình : \(x^2+2mx+4=0\)
Tìm m để pt có 2 nghiệm x1,x2 thỏa mãn : \(\left(\dfrac{x1}{x2}\right)^2+\left(\dfrac{x2}{x1}\right)^2=3\)
Phương trình có 2 nghiệm khi \(\Delta'=m^2-4\ge0\Rightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=4\end{matrix}\right.\)
\(\left(\dfrac{x_1}{x_2}\right)^2+\left(\dfrac{x_2}{x_1}\right)^2=3\)
\(\Rightarrow\left(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}\right)^2-2=3\)
\(\Rightarrow\left(\dfrac{x_1^2+x_2^2}{x_1x_2}\right)^2=5\)
\(\Rightarrow\left(\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{4}\right)^2=5\)
\(\Rightarrow\left(m^2-2\right)^2=5\)
\(\Rightarrow m^2=2+\sqrt{5}\)
\(\Rightarrow m=\pm\sqrt{2+\sqrt{5}}\)
Đúng 3
Bình luận (2)
Tìm m để phương trình x2 + (4m + 1)x + 2( m - 4 ) = 0 có hai nghiệm x1 , x1 thỏa mãn | x1 - x2 | = 17
\(\text{Δ}=\left(4m+1\right)^2-8\left(m-4\right)\)
\(=16m^2+8m+1-8m+32\)
\(=16m^2+33>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Ta có: \(\left|x_1-x_2\right|=17\)
\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=17\)
\(\Leftrightarrow\sqrt{\left(4m+1\right)^2-4\cdot2\cdot\left(m-4\right)}=17\)
\(\Leftrightarrow\sqrt{16m^2+8m+1-8m+32}=17\)
\(\Leftrightarrow16m^2+33=289\)
=>m=4 hoặc m=-4
Đúng 6
Bình luận (0)
x^2-2mx+4=0
a)giải phương trình đã cho khi m=3
b)tìm giá trị của m để pt có hai nghiệm x1 x2 thỏa mãn (x1+1)^2+(x2+1)^2=2
a, Khi m = 2
pt trở thành : x^2 - 6x + 4 = 0
<=> (x^2-6x+9) - 5 = 0
<=> (x-3)^2 = 5
<=> x=3+-\(\sqrt{5}\)
Tk mk nha
Đúng 0
Bình luận (0)
b) Câu hỏi của Mavis Dracula - Toán lớp 9 - Học toán với OnlineMath
Cho phương trình x^2 -2mx+4m-4=0 (1) , m là tham số
a)Gia phương trình với m=1
b)Tìm giá trị của m để phương trình (1) có hai nghiệm phân biệt x1,x2 thỏa mãn điều kiện x1^2 +2mx2 -8m+5=0






