`ab(x-3) -a^2(x-3)`

`=(x-3)(a^2-ab)`

__

`ax+ay+bx+by`

`=a(x+y)+b(x+y)`

`=(x+y)(a+b)`

__

`ax+ay -2x-2y`

`=(ax+ay)-(2x+2y)`

`=a(x+y)-2(x+y)`

`=(x+y)(a-2_`

__

`2x-2y +ax-ay`

`=2(x-y)+a(x-y)`

`=(x-y)(2+a)`

__

`10ax -5ay -2x+y`

`= 5a(2x-y) -(2x-y)`

`=(2x-y)(5a-1)`

1: =(x-3)(ab-a^2)

=a(b-a)(x-3)

2: =a(x+y)+b(x+y)

=(x+y)(a+b)

3: =a(x+y)-2(x+y)

=(x+y)(a-2)

4: =2(x-y)+a(x-y)

=(x-y)(a+2)

5: =5a(2x-y)-(2x-y)

=(2x-y)(5a-1)

1) \(ab\left(x-3\right)-a^2\left(x-3\right)=a\left(x-3\right)\left(b-a\right)\)

2) \(ax+ay+bx+by=\left(a+b\right)\left(x+y\right)\)

3) \(ax+ay-2x-2y=\left(a-2\right)\left(x+y\right)\)

4) \(2x-2y+ax-ay=\left(2+a\right)\left(x-y\right)\)

5) \(10ax-5ay-2x+y=5a\left(2x-y\right)-\left(2x-y\right)=\left(5a-1\right)\left(x-y\right)\)

1) x - y - a(x - y) = (x - y) - a(x - y) = (1 - x)(x - y)

2) a - b + x(a - b) = (a - b) + x(a - b) = (1 + x)(a - b)

3) a(x - y) - x + y = a(x - y) - (x - y) = (a - 1)(x - y)

4) x(a - b) - a + b = x(a - b) - (a - b) = (x - 1)(a - b)

5) ax + ay + bx + by = a(x + y) + b(x + y) = (a + b)(x + y)

6) ax + ay - bx - by = a(x + y) - b(x + y) = (a - b)(x + y)

7) - 2x - 2y + ax + ay = -2(x + y) + a(x + y) = (a - 2)(x + y)

8) x² - xy - 2x + 2y = x(x - y) - 2(x - y) = (x - 2)(x - y)

Sorry nha, giờ mình chỉ rảnh làm 8 câu thôi

Bài 4

c) x(x - 2) + (x - 2)²

= (x - 2)(x + x - 2)

= (x - 2)(2x - 2)

= 2(x - 2)(x - 1)

d) 2x(x - y)² - 5(y - x)

= 2x(x - y)² + 5(x - y)

= (x - y)(2x + 5)

Bài 5

a) x² - 6x - 2xy + 12y

= (x² - 6x) - (2xy - 12y)

= x(x - 6) - y(x - 6)

= (x - 6)(x - y)

b) 10ax - 5ay - 2x + y

= (10ax - 5ay) - (2x - y)

= 5a(2x - y) - (2x - y)

= (2x - y)(5a - 1)

c) x⁴ + x³y - x - y

= (x⁴ + x³y) - (x + y)

= x³(x + y) - (x + y)

= (x + y)(x³ - 1)

= (x + y)(x - 1)(x² + x + 1)

d) x³ + 2x² - 4x - 8

= (x³ + 2x²) - (4x + 8)

= x²(x + 2) - 4(x + 2)

= (x + 2)(x² - 4)

= (x + 2)(x + 2)(x - 2)

= (x + 2)²(x - 2)

e) xy - 5x - y² + 5y

= (xy - 5x) - (y² - 5y)

= x(y - 5) - y(y - 5)

= (y - 5)(x - y)

f) ax - bx - 2cx - 2a + 2b + 4c

= (ax - bx - 2cx) - (2a - 2b - 4c)

= x(a - b - 2c) - 2(a - b - 2c)

= (a - b - 2c)(x - 2)

g) 5x²y + 5xy² - b²x - b²y

= (5x²y + 5xy²) - (b²x + b²y)

= 5xy(x + y) - b²(x + y)

= (x + y)(5xy - b²)

h) 4x³ - 4x² - 9x + 9

= (4x³ - 4x²) - (9x - 9)

= 4x²(x - 1) - 9(x - 1)

= (x - 1)(4x² - 9)

= (x - 1)(2x - 3)(2x + 3)

từng câu 1 thôi:v

a) x2-xy+5y-25
 = x(2-y)+ 5(y-2)
 = x(2-y)-5(2-y)
 = (x-5)(2-y)

h: \(=\left(a-1-b\right)\left(a-1+b\right)\)

Bn viet bây à

Giúp mik đi

1, x(a-b)+a-b          2, x-y-a(x-y)            3, a(x+y)-x-y               4, x(a-b)-a+b         5, x²+xy-2x-2y            6, 10ax-5ay+2x-y

= x(a-b)+(a-b)           =(x-y)-a(x-y)             =a(x+y)-(x+y)             =x(a-b)-(a-b)         =(x²+xy)-(2x+2y)        =(10ax+2x)-(5ay+y)

=(a-b)(x+1)               =(x-y)(1-a)                =(x+y)(a-1)                 =(a-b)(x-1)            =x(x+y)-2(x+y)            =2x(5a+1)-y(5a+1)

                                                                                                                                  =(x+y)(x-2)                  =(5a+1)(2x-y)

7, 2a²x-5by-5a²y+2bx           8, 2ax²-bx²-2ax+bx+4a-2b             9, 2ax-bx+3cx-2a+b-3c                     10, ax-bx-2cx-2a+2b+4c

=(2a²x+2bx)-(5by+5a²y)           =(2ax²-bx²)-(2ax-bx)+(4a-2b)        =(2ax-2a)-(bx-b)+(3cx-3c)                  =(ax-2a)-(bx-2b)-(2cx-4c)

=2x(a²+b)-5y(b+a²)                   =x²(2a-b)-x(2a-b)+2(2a-b)             =2a(x-1)-b(x-1)+3c(x-1)                      =a(x-2)-b(x-2)-2c(x-2)

=(a²+b)(2x-5y)                           =(2a-b)(x²-x+2)                              =(x-1)(2a-b+3c)                                  =(x-2)(a-b-2c)

bn post nhiều nên mình ghi đáp án thôi nhé phần nào sai đề mình cho qua

b)\(\left(x+1\right)\left(xy+1\right)\)

c)\(\left(a+b\right)\left(x+y\right)\)

d)\(\left(x-a\right)\left(x-b\right)\)

e)\(\left(x+y\right)\left(xy-1\right)\)

f)\(\left(a-b\right)\left(x^2+y\right)\)

a: \(x^2\left(x-3\right)-4x+12\)

\(=x^2\left(x-3\right)-4\left(x-3\right)\)

\(=\left(x-3\right)\left(x-2\right)\left(x+2\right)\)

b: \(2a\left(x+y\right)+x+y=\left(x+y\right)\left(2a+1\right)\)

c: \(6x^2-12x-7x+14\)

\(=6x\left(x-2\right)-7\left(x-2\right)\)

\(=\left(x-2\right)\left(6x-7\right)\)

\(a,=5\left(x-y\right)+a\left(x-y\right)=\left(5+a\right)\left(x-y\right)\\ b,=a\left(x+y\right)+b\left(x+y\right)=\left(a+b\right)\left(x+y\right)\\ c,=x\left(x+1\right)+a\left(x+1\right)=\left(x+a\right)\left(x+1\right)\\ d,Sửa:x^2y+xy^2-3x-3y=xy\left(x+y\right)-3\left(x+y\right)=\left(xy-3\right)\left(x+y\right)\\ e,=xy\left(x+1\right)-\left(x+1\right)=\left(xy-1\right)\left(x+1\right)\\ f,=x^2-4=\left(x-2\right)\left(x+2\right)\\ g,=\left(x+3\right)^2-y^2=\left(x-y+3\right)\left(x+y+3\right)\\ h,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ i,=\left(x-4\right)^2-24y^2=\left(x-2\sqrt{6}y-4\right)\left(x+2\sqrt{6}y+4\right)\)

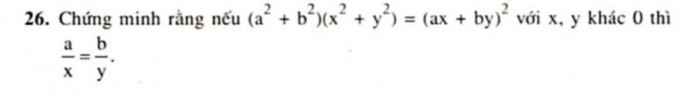
Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)

\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)

\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)

\(\Leftrightarrow\left(ay-xb\right)^2=0\)

\(\Leftrightarrow ay=xb\)

hay \(\dfrac{a}{x}=\dfrac{b}{y}\)