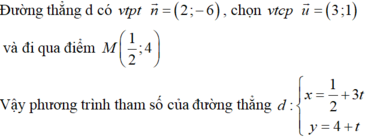pt tham số của đt \(\Delta:2x-6y+23=0\)
NT
Những câu hỏi liên quan
cho điểm A(-1;2) đt Delta 2x - y-1 0 và đtròn ( c) (x-1)^2 + (y-2)^29tìm tọa độ giao điểm a1 là ảnh của a qua Đoxtìm tọa độ điểm a2 là ảnh của a qua Đoyviết pt đt Delta^, là ảnh của Delta qua Đoxviết pt đtron ( c^,) là ảnh của (c) qua Đoygiải nhanh giúp mình với
Đọc tiếp
cho điểm A(-1;2) đt \(\Delta\) 2x - y-1 =0 và đtròn ( c) (x-1)\(^2\) + (y-2)\(^2\)=9
tìm tọa độ giao điểm a1 là ảnh của a qua Đox
tìm tọa độ điểm a2 là ảnh của a qua Đoy
viết pt đt \(\Delta^,\) là ảnh của \(\Delta\) qua Đox
viết pt đtron ( c\(^,\)) là ảnh của (c) qua Đoy
giải nhanh giúp mình với
a: Tọa độ A1 là ảnh của A qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_{A_1}=x_A=-1\\y_{A_1}=-y_A=-2\end{matrix}\right.\)
Vậy: \(A_1\left(-1;-2\right)\)
b: Tọa độ A2 là ảnh của A qua phép đối xứng trục Oy là:
\(\left\{{}\begin{matrix}x_{A_2}=-x_A=1\\y_{A_2}=y_A=2\end{matrix}\right.\)
Vậy: \(A_2\left(1;2\right)\)
c: Tọa độ giao điểm B của (Δ) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\2x-y-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Vậy: B(1/2;0)
Vì B thuộc Ox nên phép đối xứng qua trục Ox biến B thành chính nó
Lấy C(1;1) thuộc (d)
Tọa độ D là ảnh của C qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_D=x_C=1\\y_D=-y_C=-1\end{matrix}\right.\)
Vậy: D(1;-1)
Do đó: Δ' là phương trình đường thẳng đi qua hai điểm B(1/2;0); D(1;-1)
\(\overrightarrow{BD}=\left(\dfrac{1}{2};-1\right)=\left(1;-2\right)\)
=>VTPT là (2;1)
Phương trình Δ' là:
\(2\left(x-1\right)+1\left(y+1\right)=0\)
=>2x-2+y+1=0
=>2x+y-1=0
Đúng 2
Bình luận (0)
Cho đt Δ có pt: 2x-5y+2=0
a) chỉ ra 2 vtcp của đt từ đó suy ra 2vtpt của đt Δ
b) tìm tọa độ 2 điểm A, B bất kì thuộc đt Δ
c) các điểm M(4;-10), N(4;2) điểm nào thuộc đt Δ
Viết pt tham số của đt ∆ biết đt ∆ có pt x-2=0
x-2=0
=>x+0y-2=0
=>VTPT là (1;0)
=>VTCP là (0;-1) và (d) đi qua A(2;0)
Phương trình tham số là:
\(\left\{{}\begin{matrix}x=2+0t=2\\y=0+\left(-1\right)t=-t\end{matrix}\right.\)
Đúng 0
Bình luận (0)
pt tham số của đt \(\Delta:\frac{x}{5}-\frac{y}{7}=1\) là ?
Phương trình nào sau đây là phương trình tham số của đường thẳng d: 2x- 6y + 23 0.
Đọc tiếp
Phương trình nào sau đây là phương trình tham số của đường thẳng d: 2x- 6y + 23= 0.
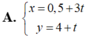
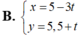
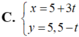
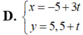
câu 1: viết pt tham số của đường thẳng Δ: 2x-5y+4=0
câu 2: viết phương trình tham số và pt tổng quát của đưởng thẳng Δ đi qua A(3;7) và Δ vuông góc với đường thẳng Δ1 có phương trình x+y-3=0
trong mặt phẳng tọa độ Oxy cho đường tròn (c): \(x^2+y^2+2x-6y+5=0.\) gọi \(\Delta\) là tiếp tuyến của (c) tại điểm A(0;1).tìm pt tổng quát của \(\Delta\)
Vì `(C): x^2+y^2+2x-6y+5=0`
`=>I(-1;3)`
Ta có: `\vec{IA}=(1;-2)`
`=>\vec{n_{\Delta}}=(1;-2)`
Mà `A(0;1) in \Delta`
`=>` PTTQ của `\Delta` là: `x-2(y-1)=0<=>x-2y+2=0`
Đúng 1
Bình luận (0)
viết phương trình tham số của đường thẳng delta biết đg thẳng có pt 2x+3y-6=0
(Δ): 2x+3y-6=0
Lấy A(3;0) thuộc (Δ)
VTPT là (2;3)
=>VTCP là (-3;2)
Phương trình tham số là:
\(\left\{{}\begin{matrix}x=3-3t\\y=0+2t=2t\end{matrix}\right.\)
Đúng 0
Bình luận (0)
cho đt Delta có pt tham số x-2+3t y-7-5ta) tìm vecto 1 chỉ phương và 1 vecto pháp tuyến của đtb) tìm tọa độ điểm H trên Delta có hoành độ 14c) tìm điểm G trên Delta có tung độ -12d) tìm tọa độ trung điểm của đoạn thẳng HG
Đọc tiếp
cho đt \(\Delta\) có pt tham số \(x=-2+3t\)
\(y=-7-5t\)
a) tìm vecto 1 chỉ phương và 1 vecto pháp tuyến của đt
b) tìm tọa độ điểm H trên \(\Delta\) có hoành độ = 14
c) tìm điểm G trên \(\Delta\) có tung độ = -12
d) tìm tọa độ trung điểm của đoạn thẳng HG
a: VTCP là (3;-5)
=>VTPT là (5;3)
b: 3t-2=14
=>3t=16
=>t=16/3
=>y=-7-5t=-7-80/3=-101/3
c: -5t-7=-12
=>5t+7=12
=>t=1
=>x=-2+3=1
d: H(14;-101/3); G(1;-12)
Tọa đọ trung điểm là:
\(\left\{{}\begin{matrix}x=\dfrac{14+1}{2}=\dfrac{15}{2}\\y=\dfrac{1}{2}\left(-\dfrac{101}{3}-12\right)=-\dfrac{137}{6}\end{matrix}\right.\)
Đúng 2
Bình luận (0)