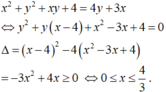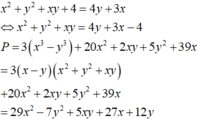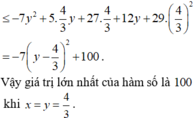Cho 3x-4y=0. Tìm giá trị nhỏ nhất của biểu thức x2+y2
NH
Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của biểu thức:
a, 3x2 – 3x + 1
b, x2 – 2x + y2 + 4y + 6
c, 2x2 + y2 – 2xy + 1
\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sau:
a) M = x 2 – 3x + 10;
b) N = 2 x 2 + 5 y 2 + 4xy + 8x – 4y – 100.
a) Từ M = x − 3 2 2 + 31 4 ≥ 31 4 ⇒ M min = 31 4 ⇔ x = 3 2 .
b) Ta có N = ( x + 2 y ) 2 + ( y – 2 ) 2 + ( x + 4 ) 2 – 120 ≥ - 120 .
Tìm được N min = -120 Û x = -4 và y = 2.
Đúng 0
Bình luận (0)
Cho số thực x, y thỏa mãn
x
2
+
y
2
+
x
y
4
y
−
1
+
3
x
. Tìm giá trị lớn nhất của biểu thức
P
3
x
3
−
y
3...
Đọc tiếp
Cho số thực x, y thỏa mãn x 2 + y 2 + x y = 4 y − 1 + 3 x . Tìm giá trị lớn nhất của biểu thức P = 3 x 3 − y 3 + 20 x 2 + 2 x y + 5 y 2 + 39 x
A. 120 2
B. 110
C. 100
D. 96 3
Đáp án C
G T ⇔ x 2 + y − 3 x + y 2 − 4 y + 4 = 0 y 2 + x − 4 y + x 2 − 3 x + 4 = 0
có nghiệm ⇔ Δ x ≥ 0 Δ y ≥ 0 ⇔ 0 ≤ x ≤ 4 3 1 ≤ y ≤ 7 3
Và:
x y = 3 x + 4 y − x 2 − y 2 − 4 ⇒ P = 3 x 3 + 18 x 2 + 45 x − 8 ⏟ f x + − 3 y 3 + 3 y 2 + 8 y ⏟ g y
Xét hàm số f x = 3 x 3 + 18 x 2 + 45 x − 8 trên 0 ; 4 3 ⇒ max 0 ; 4 3 f x = f 4 3 = 820 9
Xét hàm số g x = − 3 y 3 + 3 y 2 + 8 y trên 1 ; 7 3 ⇒ max 1 ; 7 3 g x = f 4 3 = 80 9
Vật P ≤ max 0 ; 4 3 f x + max 1 ; 7 3 g x = 100
Dấu “=” xảy ra khi x = y = 4 3
Đúng 0
Bình luận (0)
Cho x,y là hai số thực thỏa mãn điều kiện
x
2
+
y
2
+
x
y
+
4
4
y
+
3
x
. Tìm giá trị lớn nhất của biểu thức
P
3
(
x...
Đọc tiếp
Cho x,y là hai số thực thỏa mãn điều kiện x 2 + y 2 + x y + 4 = 4 y + 3 x . Tìm giá trị lớn nhất của biểu thức P = 3 ( x 3 - y 3 ) + 20 x 2 + 2 x y + 5 y 2 + 39 x .
![]()
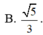
![]()
cho hai số thực x>0,y>0 thoả mãn xy=6.Tìm giá trị nhỏ nhất của biểu thức P=x2+y2
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
Đúng 1
Bình luận (0)
tìm giá trị nhỏ nhất của các biểu thức sau :
a,M=x2-3x+10
b,N=2x2+5y2+4xy+8x-4y-100
a) \(M=x^2-3x+10\)
\(M=x^2-2\cdot\dfrac{3}{2}\cdot x+\dfrac{9}{4}+\dfrac{31}{4}\)
\(M=\left(x^2-2\cdot\dfrac{3}{2}\cdot x+\dfrac{9}{4}\right)+\dfrac{31}{4}\)
\(M=\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}\)
Mà: \(\left(x-\dfrac{3}{2}\right)^2\ge0\) nên: \(M=\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}\ge\dfrac{31}{4}\)
Dấu "=" xảy ra
\(\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}=\dfrac{31}{4}\Leftrightarrow\left(x-\dfrac{3}{2}\right)^2=0\)
\(\Leftrightarrow x-\dfrac{3}{2}=0\Leftrightarrow x=\dfrac{3}{2}\)
Vậy: \(M_{min}=\dfrac{31}{4}\) với \(x=\dfrac{3}{2}\)
b) \(N=2x^2+5y^2+4xy+8x-4y-100\)
\(N=x^2+x^2+4y^2+y^2+4xy+8x-4y-120+16+4\)
\(N=\left(x^2+4xy+4y^2\right)+\left(x^2+8x+16\right)+\left(y^2-4y+4\right)-120\)
\(N=\left(x+2y\right)^2+\left(x+4\right)^2+\left(y-2\right)^2-120\)
Mà:
\(\left\{{}\begin{matrix}\left(x+2y\right)^2\ge0\\\left(x+4\right)^2\ge0\\\left(y-2\right)^2\ge0\end{matrix}\right.\) nên \(N=\left(x+2y\right)^2+\left(x+4\right)^2+\left(y-2\right)^2-120\ge120\)
Dấu "=" xảy ra:
\(\left\{{}\begin{matrix}\left(x+2y\right)^2=0\\\left(x+4\right)^2=0\\\left(y-2\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-4+2y=0\\x=-4\\y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=-4\\y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=2\end{matrix}\right.\)
Vậy: \(N_{min}=120\) khi \(\left\{{}\begin{matrix}x=-4\\y=2\end{matrix}\right.\)
Đúng 2
Bình luận (1)
a
\(M=x^2-3x+10=x^2-2.\dfrac{3}{2}.x+\dfrac{9}{4}+\dfrac{31}{4}\\ =\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}\ge\dfrac{31}{4}\)
Min M \(=\dfrac{31}{4}\) khi và chỉ khi \(x=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
b
\(N=2x^2+5y^2+4xy+8x-4y-100\\ =x^2+8x+16+y^2-4y+4+x^2+4xy+4y^2-120\\ =\left(x+4\right)^2+\left(y-2\right)^2+\left(x+2y\right)^2-120\ge-120\)
Min N \(=-120\) khi và chỉ khi \(x=-4\) và \(y=2\)
Đúng 1
Bình luận (0)
cho 3x-4y=0 Tìm giá trị nhỏ nhất của biểu thức M=x^2+y^2
Biểu thức
K
x
2
–
6
x
+
y
2
–
4
y
+
6
có giá trị nhỏ nhất là A. 6 B. 1 C. -7 D. 7
Đọc tiếp
Biểu thức K = x 2 – 6 x + y 2 – 4 y + 6 có giá trị nhỏ nhất là
A. 6
B. 1
C. -7
D. 7
Ta có
K = x 2 – 6 x + y 2 – 4 y + 6 = x 2 – 2 x . 3 + 9 + y 2 – 2 . y . 2 + 4 – 7 = ( x – 3 ) 2 + ( y – 2 ) 2 – 7
Vì ( x – 3 ) 2 ≥ 0 ; ( y – 2 ) 2 ≥ 0 ; Ɐx; y nên ( x – 3 ) 2 + ( y – 2 ) 2 – 7 ≥ -7
Dấu “=” xảy ra khi ó x − 3 2 = 0 và y − 2 2 = 0 hay x = 3 và y = 2
Vậy giá trị nhỏ nhất của K là -7 khi x = 3; y = 2
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất của biểu thức : P=-x2-y2+4x-4y+2
\(P=-x^2-y^2+4x-4y+2=-\left(x^2-4x+4\right)-\left(y^2+4y+4\right)+10=-\left(x-2\right)^2-\left(y+2\right)^2+10\le10\)
Dấu = xảy ra khi x = 2; y = -2
Đúng 1
Bình luận (0)
Tính giá trị nhỏ nhất của các biểu thức sau:
a) A = 4x2 +4x + 11
b) C = x2 - 2x + y2 - 4y + 7
Lời giải:
a)
$A=4x^2+4x+11=(4x^2+4x+1)+10=(2x+1)^2+10\geq 10$
Vậy $A_{\min}=10$. Giá trị này đạt tại $(2x+1)^2=0$
$\Leftrightarrow x=-\frac{1}{2}$
b)
$C=x^2-2x+y^2-4y+7=(x^2-2x+1)+(y^2-4y+4)+2$
$=(x-1)^2+(y-2)^2+2\geq 2$
Vậy $C_{\min}=2$. Giá trị này đạt tại $(x-1)^2=(y-2)^2=0$
$\Leftrightarrow x=1; y=2$
Đúng 0
Bình luận (0)