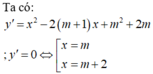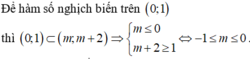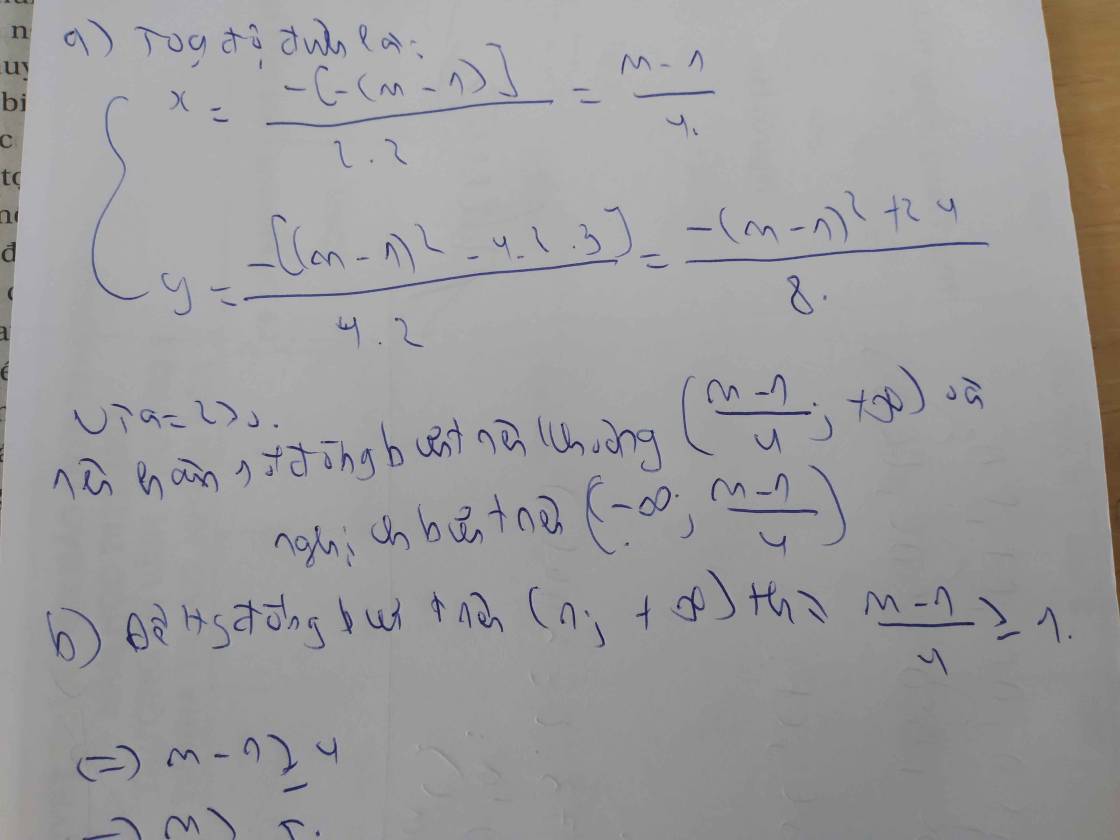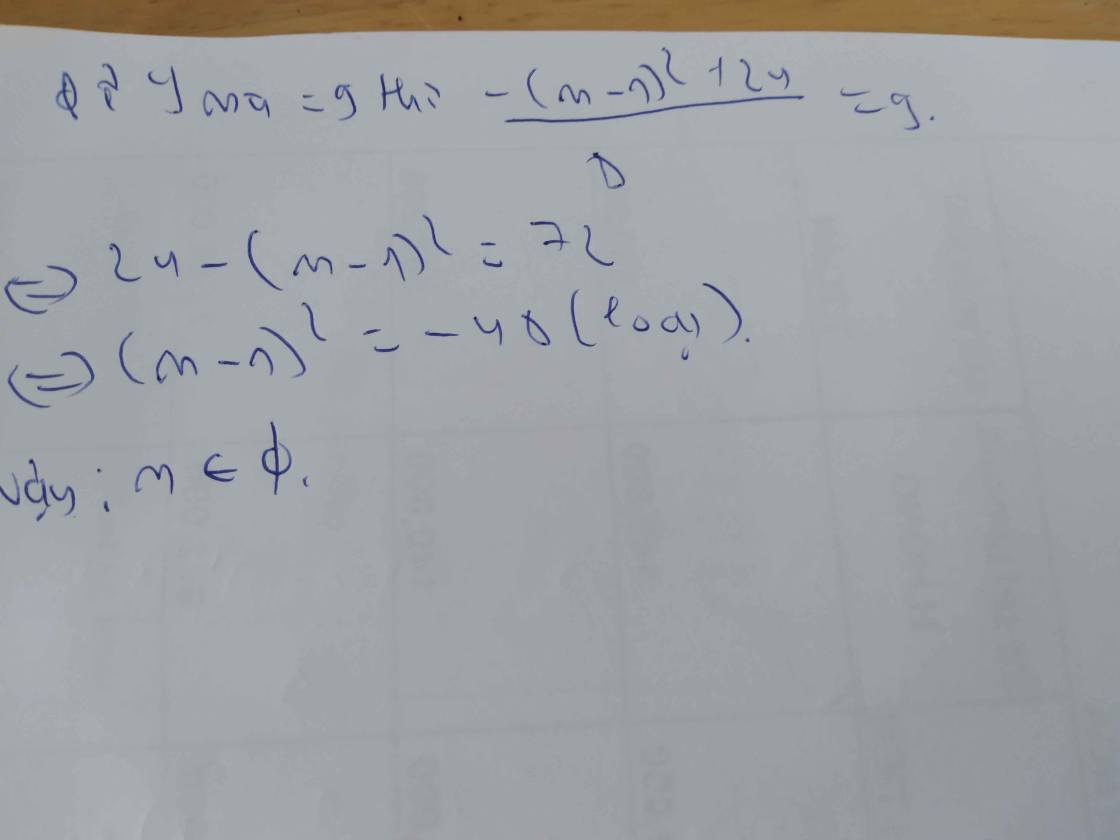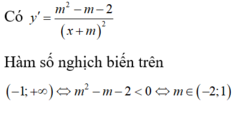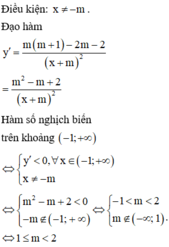tìm các giá trị của m để hàm số y=(m2-1)x + 2m-1 nghịch biến trên khoảng (-4;3)
TZ
Những câu hỏi liên quan
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
2...
Đọc tiếp
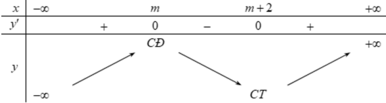
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng ( 0 ; 1 )
A. [ - 1 ; + ∞ )
B. ( - ∞ ; 0 ]
C. [ - 1 ; 0 ]
D. [ 0 ; 1 ]
Tập hợp S tất cả các giá trị của tham số thực m để hàm số: y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
2
+
2
m
)
x
-
3
nghịch biến trên khoảng (-1;1) là A. S
∅...
Đọc tiếp
Tập hợp S tất cả các giá trị của tham số thực m để hàm số: y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng (-1;1) là
A. S = ∅
B. S = [0;1]
C. S = [-1;0]
D. S = {-1}
Chọn D.
![]()
Do đó ta có bảng biến thiên sau:
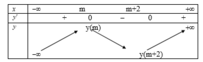
Để hàm số nghịch biến trên khoảng (-1;1) thì
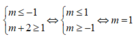
Đúng 0
Bình luận (0)
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9
Tìm tất cả các giá trị thực của tham số m để hàm số
y
m
+
1
x
+
2
m
+
2
x
+
m
nghịch biến trên khoảng
−
1
;
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = m + 1 x + 2 m + 2 x + m nghịch biến trên khoảng − 1 ; + ∞ .
A. − 1 < m < 2
B. m ≥ 1
C. m < 1 m > 2
D. 1 ≤ m < 2
Tìm tất cả các giá trị thực của tham số m để hàm số
y
m
+
1
x
+
2
m
+
2
x
+
m
nghịch biến trên khoảng
−
1
;
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = m + 1 x + 2 m + 2 x + m nghịch biến trên khoảng − 1 ; + ∞ .
A. − 1 < m < 2
B. m ≥ 1
C. m < 1 m > 2
D. 1 ≤ m < 2
Đáp án A
Có y ' = m 2 − m − 2 x + m 2 . Hàm số nghịch biến trên − 1 ; + ∞ ⇔ m 2 − m − 2 < 0 ⇔ m ∈ − 2 ; 1
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{2m-x}{x-3}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{x+3}{x+m}\) nghịch biến trên từng khoảng xác định
a: TXĐ: D=R\{3}
\(y=\dfrac{2m-x}{x-3}\)
=>\(y'=\dfrac{\left(2m-x\right)'\left(x-3\right)-\left(2m-x\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
\(=\dfrac{-\left(x-3\right)-2m+x}{\left(x-3\right)^2}\)
\(=\dfrac{3-2m}{\left(x-3\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì y'>0 với mọi x thỏa mãn ĐKXĐ
=>\(\dfrac{3-2m}{\left(x-3\right)^2}>0\)
=>3-2m>0
=>2m<3
=>\(m< \dfrac{3}{2}\)
b: TXĐ: D=R\{-m}
\(y=\dfrac{x+3}{x+m}\)
=>\(y'=\dfrac{\left(x+3\right)'\left(x+m\right)-\left(x+3\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{x+m-x-3}{\left(x+m\right)^2}=\dfrac{m-3}{\left(x+m\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\in TXĐ\)
=>\(\dfrac{m-3}{\left(x+m\right)^2}< 0\)
=>m-3<0
=>m<3
Đúng 0
Bình luận (0)
Tìm các giá trị của m để hàm số
y
2
-
x
-
2
2
-
x
-
m
nghịch biến trên khoảng (-1; 1) A.
m
≤
1
2
,
m...
Đọc tiếp
Tìm các giá trị của m để hàm số y = 2 - x - 2 2 - x - m nghịch biến trên khoảng (-1; 1)
A. m ≤ 1 2 , m > 2
B. m ≤ 1 2
C. m > 2
D. m ≤ 2
Tìm các giá trị của tham số m để hàm số y=1/3x^3-mx^2+(2m-1)x-m+2 nghịch biến trên khoảng (-2;0)
giúp em với ạ .
Bạn tham khảo, nguồn mạng :

Ps : không thấy ảnh ib, nhớ k ạ
# Aeri #
Tìm tất cả các giá trị của tham số m để hàm số \(y=\left(m^2-6m\right)x-\sqrt{2m-3}\)nghịch biến trên khoảng (-3; 5)
Tìm các giá trị thực của tham số m sao cho hàm số
y
m
+
1
x
+
2
m
+
2
x
+
m
nghịch biến trên khoảng
-
1
;
+...
Đọc tiếp
Tìm các giá trị thực của tham số m sao cho hàm số y = m + 1 x + 2 m + 2 x + m nghịch biến trên khoảng - 1 ; + ∞ .
A. m ≥ 1
B. m ∈ - ∞ ; 1 ∪ 2 ; + ∞
C. - 1 ≤ m < 2
D. -1 < m < 2