cho góc nhọn xOy.Lấy A,B thuộc Ox C,D thuộc Oy sao cho OA=OC,OB=OD
chứng minh AD=BC
Cho góc xOy nhọn; A, B thuộc Ox; C, D thuộc Oy. Sao cho OA = OC; OB = OD; AD cắt BC tại I Chứng minh: a, tam giác OAD = tam giác OCB b, IA = IC c, OI Vuông góc với BD
a)Xét ΔOAD và ΔOCB
Có: OA = OC (gt)
OD =OB (gt)
∠O là góc chung
⇒ ΔOAD = ΔOCB (c.g.c)
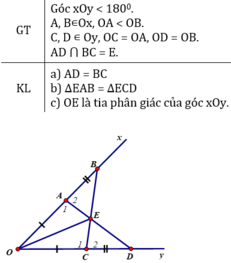
Bài 1: Cho góc xOy khác góc bẹt lấy các điểm A, B thuộc tia Ox sao cho OA < OB.
Lấy điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB.
Gọi E là giao điểm của AD và BC. Chứng minh:
a) AD = BC b) DEAB = DECD c) OE là phân giác của góc xOy
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
AD = BC
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
Cho góc XOY bé hơn 90°. Lấy điểm a,b thuộc tia ox sao cho OA bé hơn OB. Lấy các điểm C,D thuộc Oy sao cho Oc bé hơn Od và Oc=Oa; Od=Ob Gọi E là giao điểm của AD và BC, chứng minh: a, AD=BC b, tam giác EAB=tâm giác ECD
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
\(a,\left\{{}\begin{matrix}OA=OC\\OD=OB\\\widehat{AOB}\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\\ \Rightarrow AD=BC\\ b,\Delta AOD=\Delta COB\\ \Rightarrow\widehat{ADO}=\widehat{CBO};\widehat{OAD}=\widehat{OCB}\\ \Rightarrow180^0-\widehat{OAD}=180^0-\widehat{OCB}\\ \Rightarrow\widehat{ECD}=\widehat{EAB}\\ \text{Ta có}\left\{{}\begin{matrix}OA=OC\\OD=OB\end{matrix}\right.\Rightarrow CD=OD-OC=OB-OA=AB\\ \left\{{}\begin{matrix}AB=CD\\\widehat{ADO}=\widehat{CBO}\\\widehat{ECD}=\widehat{EAB}\end{matrix}\right.\Rightarrow\Delta EAB=\Delta ECD\left(g.c.g\right)\)
Cho góc nhọn xoy.Lấy A,B trên oy sao cho OA=5cm,OB=16cm.Lấy C,D trên ox sao cho OC=8cm,OD=10cm có AD và BC cắt nhau tại I.Chứng minh rằng a)∆OCB~∆OAD
b)∆IAB và ∆ICD có các góc bằng nhau từng đôi 1
a: Xét ΔOCB và ΔOAD có
OC/OA=OB/OD
\(\widehat{COB}\) chung
Do đó: ΔOCB∼ΔOAD
b: \(\widehat{AIB}=\widehat{CID}\)(đối đỉnh)
\(\widehat{IBA}=\widehat{IDC}\)(ΔOCB∼ΔOAD)
\(\widehat{IAB}=\widehat{ICD}\)
Cho góc xOy là góc nhọn, có A thuộc Ox, B thuộc Oy sao cho OA=OB, C thuộc Ox, D thuộc Oy sao cho OC=OD. CM:
a) AD=BC
b)Gọi E là giao điểm AD và BC vậy tam giác AEC bằng tam giác BED
a) Xét hai tam giác OAD và OBC :
OA = OB ( gt )
OC = OD ( gt )
O là góc chung
=> tam giác OAD = OBC ( c.g.c)
b) Ta có :
A1 + A2 = 180
B1 + B2 = 180
mà A1 = B1 ( vì tam giác OAD = OBC )
=> A2 = B2
Xét hai tam giác ACE và tam giác BDE :
^C = ^D ( tam giác OAD = OBC )
A2 = B2 ( cmt )
ta có : OC= OA + AC
OD = OB + BD
mà OA = OB ( gt )
OC = OD ( gt)
=> AC = BD
=> tam giác ACE = BDE ( g.c.g )
a: Xét ΔOAD và ΔOCB có
OA=OC
góc AOD chung
OD=OB
=>ΔOAD=ΔOCB
=>AD=CB
b: Xét ΔEAB và ΔECD có
góc EAB=góc ECD
AB=CD
góc EBA=góc EDC
=>ΔEAB=ΔECD
c: Xét ΔOAE và ΔOCE có
OA=OC
AE=CE
OE chung
=>ΔOAE=ΔOCE
=>góc AOE=góc COE
=>góc AOM=góc CON
Xét ΔCON và ΔAOM có
góc CON=góc AOM
CO=AO
góc OCN=góc OAM
=>ΔCON=ΔAOM
=>ON=OM
=>ΔENM can tại E
=>EM=EN
=>NC=MA
Xét ΔEMB và ΔEND có
EM=EN
góc MEB=góc NED
EB=ED
=>ΔEMB=ΔEND
=>ND=MB và góc EMB=góc END
=>góc KMO=góc KNO
=>ΔKMN cân tại K
KD+DN=KN
KB+BM=KM
mà KM=KN; DN=BM
nên KD=KB
=>K nằm trên trung trực của DB(1)
OB=OD
nên O nằm trên trung trực của DB(2)
EB=ED
nên E nằm trên trung trực của DB(3)
Từ (1), (2), (3) suy ra O,E,K thẳng hàng
Cho góc xoy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA< OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC chứng minh rằng. A) AD= BC B) ∆EAB= ∆ECD C)OE là tia phân giác của góc xOy. Giải giúp e câu C với ạ.
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy
Cho x O y ^ . Lấy các điểm A,B thuộc tia Ox sao cho OA > OB. Lấy các điểm C, D thuộc Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh:
a) AD = BC ;
b) ∆ A B E = ∆ C D E ;
c) OE là tia phân giác của góc xOy.