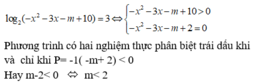Tìm tất cả các giá trị của m để phương trìng ( x2 + 3x - m) (x+2)=0 có 3 nghiệm phân biệt.
NN
Những câu hỏi liên quan
Cho phương trình: x2-(m-1)x-m-2=0. Tìm tất cả các giá trị của m để pt có 2 nghiệm phân biệt x1, x2 thỏa mãn x2+x1-x2=4-m
Tìm tất cả các giá trị thực của m để phương trình log2( -x2 - 3x – m + 10) = 3 có nghiệm thực phân biệt trái dấu.
A. m < 4
B. m > 2
C. m < 2
D. m > 4
Cho phương trình: x 2 - 2(m - 3)x + 5 - m = 0
a) Giải phương trình khi m = 1.
b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn x1 < x2 < 1.
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0 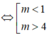
Do x1 < x2 < 1
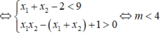
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để phương trình \(x^2-\left(m-1\right)x+\left(m+3\right)=0\) có 2 nghiệm phân biệt x1, x2 thỏa mãn \(x_1^2+x_2^2\) đạt giá trị nhỏ nhất.
\(\Delta=\left(m-1\right)^2-4\left(m+3\right)=m^2-6m-11>0\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=m+3\end{matrix}\right.\)
Ta có:
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m-1\right)^2-2\left(m+3\right)=m^2-4m-5\)
Biểu thức này ko tồn tại cả min lẫn max với điều kiện m từ (1)
Đúng 1
Bình luận (0)
Cho phương trình: x²-4x+m-5=0
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn: (x1-1)(x2²-3x2+m-6)=-3
1.Cho phương trình x2 +4x-m=0(1).Tìm tất cả các giá trị của tham số m để phương trinh (1) có đúng 1 nghiệm thuộc khoảng (-3,1)
2.Có bao nhiêu giá trị m nguyên trong nửa khoảng (0;2019] để phương trình |x2 -4|x|-5|-m có hai nghiệm phân biệt
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
Đúng 0
Bình luận (0)
Cho phương trình \(x^2-2\left(m+1\right)x+m^2+2m=0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1,x2(x1<x2)
thoa man: \(\left|x1\right|=3\left|x2\right|\)
\(\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=m+1-1=m\\x_2=m+1+1=m+2\end{matrix}\right.\)
\(\left|x_1\right|=3\left|x_2\right|\Leftrightarrow\left|m\right|=3\left|m+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3m+6=-m\\3m+6=m\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-3\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho phương trình x^2 - 4x + 3 -m 0 có hai nghiệm phân biệt x1;x2 sao cho 0≤x1x23
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho phương trình x^2 - 4x + 3 -m = 0 có hai nghiệm phân biệt x1;x2 sao cho 0≤x1<x2<3
Lời giải:
Để pt có 2 nghiệm pb thì: $\Delta'=4-(3-m)>0$
$\Leftrightarrow m+1>0\Leftrightarrow m>-1(*)$
Khi đó, áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt thì:
$x_1+x_2=4$
$x_1x_2=3-m$
Để $0\leq x_1< x_2<3$ thì:
\(x_2,x_1\geq 0\Leftrightarrow \left\{\begin{matrix}\ x_1x_2=3-m\geq 0\\ x_1+x_2=4\geq 0\end{matrix}\right.\Leftrightarrow m\leq 3(**)\)
\(x_2,x_2<3\Leftrightarrow \left\{\begin{matrix} x_1+x_2<6\\ (x_1-3)(x_2-3)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4<6\\ x_1x_2-3(x_1+x_2)+9>0\end{matrix}\right.\)
\(\Leftrightarrow 3-m-12+9>0\Leftrightarrow m<0(***)\)
Từ $(*); (**); (***)\Rightarrow -1< m< 0$
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình
x
2
+
2
m
x
-
m
-
1
0
có 2 nghiệm phân biệt x1,x2 sao cho
x
1
2
+
x
2
2
2
A. m-1/2 hoặc m0 B. m0 C. m-1/2 D. m1/2 hoặc m0
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình x 2 + 2 m x - m - 1 = 0 có 2 nghiệm phân biệt x1,x2 sao cho x 1 2 + x 2 2 = 2
A. m=-1/2 hoặc m=0
B. m=0
C. m=-1/2
D. m=1/2 hoặc m=0
Tìm tất cả giá trị của m để phương trình
x
4
-
2
(
m
+
1
)
x
2
+
m
2
-
3
0
có 4 nghiệm thực phân biệt?
A
.
(
3
;
+
∞
)
B
.
[
3...
Đọc tiếp
Tìm tất cả giá trị của m để phương trình x 4 - 2 ( m + 1 ) x 2 + m 2 - 3 = 0 có 4 nghiệm thực phân biệt?
A . ( 3 ; + ∞ )
B . [ 3 ; + ∞ )
C . ( 1 ; 6 )
D . [ 1 ; 6 )