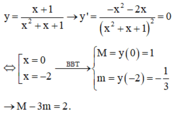giá trị nhỏ nhất của hàm số \(y=x-2\sqrt{x+2}\) là bao nhiêu
NB
Những câu hỏi liên quan
Gọi M,m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y=\(\sqrt{1+x}+\sqrt{1-x}\). Giá trị của M+m là
A.4 B.2+\(\sqrt{2}\) C.4+\(\sqrt{2}\) D.2
Cho hàm số y = -0,75x2. Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
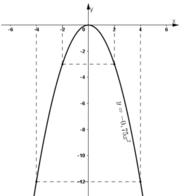
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.
Đúng 0
Bình luận (0)
Cho hàm số y = - 0 , 75 x 2 . Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = - 0 , 75 x 2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
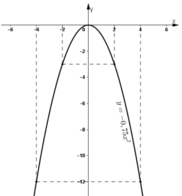
- Quan sát đồ thị hàm số y = - 0 , 75 x 2 :
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.
Đúng 0
Bình luận (0)
Gọi M,m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y=\(\sqrt{1+x}+\sqrt{1-x}\). Giá trị của M+m là
A.4 B.2+\(\sqrt{2}\) C.4+\(\sqrt{2}\) D.2
Giải thích hộ em với
Cho hàm số y = -0,75x2. Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
Vẽ đồ thị: y = -0,75x2
| x | -4 | -2 | -1 | 0 | 1 | 2 | 4 |
| y=-0,75x2 | -12 | -3 | -0,75 | 0 | -0,75 | -3 | -12 |
Vì -2 < 0 < 4 và khi x = 0 thì y = 0 là giá trị lớn nhất của hàm số. Hơn nữa khi x = -2 thì y = -0,75 . (-2)2 = -3, khi x = 4 thì y = -0,75 . (4)2 = -12 < -3
Do đó khi -2 ≤ x ≤ 4 thì giá trị nhỏ nhất của hàm số là -12 còn giá trị lớn nhất là 0.
Đúng 0
Bình luận (0)
Cho hàm số y = -0,75x2 . Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu ?
Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\), có bao nhiêu giá trị nguyên của tham số a \(\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
Cho hàm số
y
m
sin
x
+
1
cos
x
+
2
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để giá trị nhỏ nhất của y nhỏ hơn -1 A. 6 B. 3 C. 4 D. 5
Đọc tiếp
Cho hàm số y = m sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để giá trị nhỏ nhất của y nhỏ hơn -1
A. 6
B. 3
C. 4
D. 5
Cho hàm số : \(y=\sqrt{\frac{x^2}{4}+\sqrt{x^2-4}}+\sqrt{\frac{x^2}{4}-\sqrt{x^2-4}}\)
Tìm giá trị nhỏ nhất của hàm số
\(y=\sqrt{\frac{x^2}{4}+\sqrt{x^2-4}}+\sqrt{\frac{x^2}{4}-\sqrt{x^2-4}}\) Điều kiện: \(x\ge2\)
\(\Rightarrow2y=2.\sqrt{\frac{x^2}{4}+\sqrt{x^2-4}}+2.\sqrt{\frac{x^2}{4}-\sqrt{x^2-4}}\)
\(=\sqrt{x^2+4\sqrt{x^2-4}}+\sqrt{x^2-4\sqrt{x^2-4}}\)
\(=\sqrt{x^2-4+4\sqrt{x^2-4}+4}+\sqrt{x^2-4-4\sqrt{x^2-4}+4}\)
\(=\sqrt{\left(\sqrt{x^2-4}+2\right)^2}+\sqrt{\left(\sqrt{x^2-4}-2\right)^2}\)
\(=\left|\sqrt{x^2-4}+2\right|+\left|\sqrt{x^2-4}-2\right|\)
\(=\sqrt{x^2-4}+2+\left|\sqrt{x^2-4}-2\right|\)(1)
TH1: \(\sqrt{x^2-4}-2\ge0\Rightarrow\sqrt{x^2-4}\ge2\Rightarrow x^2-4\ge4\Rightarrow x\ge2\sqrt{2}\).Ta có:
\(\left(1\right)=\sqrt{x^2-4}+2+\sqrt{x^2-4}-2=2\sqrt{x^2-4}\)
Do \(x\ge2\sqrt{2}\Rightarrow2\sqrt{x^2-4}\ge2\sqrt{\left(2\sqrt{2}\right)^2-4}=4\)
TH2: \(\sqrt{x^2-4}-2< 0\Rightarrow\sqrt{x^2-4}< 2\Rightarrow x^2-4< 4\Rightarrow x^2< 8\Rightarrow2\le x< 2\sqrt{2}\).Ta có:
\(\left(1\right)=\sqrt{x^2-4}+2-\sqrt{x^2-4}+2=4\)
Vậy GTNN của y bằng 4.
Dấu "=" xảy ra khi \(2\le x\le2\sqrt{2}\)
Đúng 0
Bình luận (0)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 1 x 2 + x + 1 . Giá trị của M - 3m bằng bao nhiêu?
A. 0
B. 1
C. -1
D. 2