Giải các câu dưới đây:
(kèm vẽ hình minh họa vị trí điểm M) (cảm ơn nhiều ạ)

các cụ có kinh nghiệm dùng lao để đánh cá dưới nước lại ko phóng to trực tiếp vào con cá dưới nc mà lại nhắm vào vị trí hơi sâu hơn 1 chút . E m hãy trình bày quan điểm của mk về cách lm này giải thích , vẽ hình minh họa

Ai giúp mình phần 2 nhỏ bài tìm gtri nguyên n với câu 3 bài hình đc ko ạ(kèm vẽ hình) nếu cần thiết mn làm giúp e câu 5 ạ ko thì thôi ạ. Mình cảm ơn nhiều
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
Khai thác atlat địa lý Việt Nam trang 15 , nêu đặc điểm dân số nước ta( đi kèm với số liệu minh họa )
Đây là bài tập địa lý 9 nhé ! Làm ơn giúp mình với !!! Cảm ơn nhiều !!!
đây là bài tập ngoài chương trình học trong sách
câu 1 nêu các loại hình đã học .Vẽ hình minh họa
câu 2 nêu mối quan hệ giữa điểm và đường thẳng .Vẽ hình minh họa,kí hiệu
câu3 thế nào là ba điểm thẳng hàng . Quan hệ giữa ba điểm thẳng hàng
câu4 vị trí tương đối của hai đường thẳng .Vẽ hình minh họa
câu5 định nghĩa hai tia đối nhau .vẽ hình ,gọi tên
định nghĩa hai tia trùng nhau.vẽ hình ,gọi tên
định nghĩa tia.vẽ hình ,gọi tên
câu6 định nghĩa đường thẳng.Vẽ hình minh họa
kể tên các trường hợp cắt đoạn thẳng ,cắt tia ,cắt đường thẳng
câu7 khi nào điểm M nằm giữa hai điểm A và B Vẽ hình minh họa
câu8 định nghĩa ,tính chất ,cách chứng minh trung điểm của đoạn thẳng
ĐM con chó Mày giim hàng tao hơi bị kinh rồi đấy
Cho tam giác ABC có góc A=90, AB=3cm, BC=10cm. D là một điểm thuộc cạnh BC, I là trung điểm của cạnh AC, E là điểm đối xứng với D qua I.
a) Điểm D ở vị trí nào trên BC thì AECD là hình chữ nhật? Giải thích? Vẽ hình minh họa.
b) Điểm D ở vị trí nào trên BC thì AECD là hình thoi? Giải thích? Vẽ hình minh họa và tính độ dài cạnh của hình thoi.
✨mn giúp mik zới ạ cảm ơn nhìu :333✨
Câu hỏi 1: Nêu khái niệm về hình chiếu? Tên gọi, hướng chiếu và vị trí của các hình chiếu ở trên bản vẽ như thế nào?
Câu hỏi 2 : Hãy nêu đặc điểm hình chiếu của khối đa diện? đặc điểm 1 số khối đa diện?
Câu hỏi 3 : Thế nào là hình cắt? Hình cắt dùng để làm gì? Các bước thu được hình cắt?
Câu hỏi 4: Hình chiếu các khối tròn xoay cơ bản?
Câu hỏi 5: Kể tên một số bản vẽ thường dùng và công dụng của chúng?
Câu hỏi 6: Thế nào là bản vẽ chi tiết? Nêu trình tự đọc bản vẽ chi tiết.
Câu hỏi 7: Ren dùng để làm gì? Quy ước vẽ ren như thế nào?
Câu hỏi 8: So sánh nội dung bản vẽ lắp với bản vẽ chi tiết.
Câu hỏi 9: Bản vẽ nhà gồm những nội dung gì? Nêu trình tự đọc bản vẽ nhà.
mọi người giúp em giải bài này với..em cảm ơn (có kèm hình vẽ ạ )
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
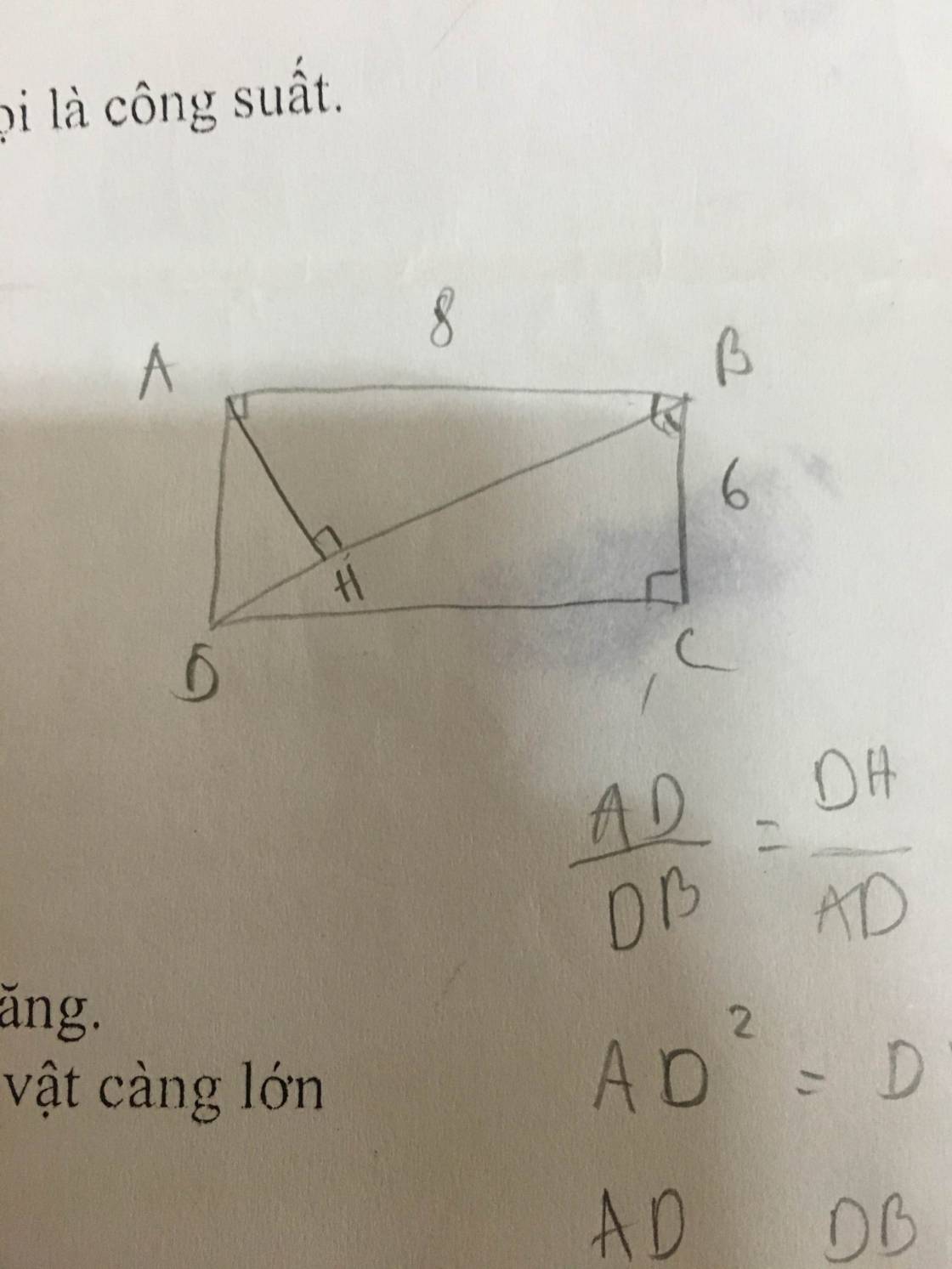
Mọi người giúp em làm bài toán hình này với ạ, kèm vẽ hình luôn nhé ạ. Em cảm ơn nhiều. - Cho hình chữ nhật ABCD có AB=8cm, BC= 6cm. Vẽ đường cao AH của tam giác ABD. a) chứng minh tam giác HBA đồng dạng với tam giác CDB b) Chứng minh: AD^2 = DH. DB c) Tính độ dài đoạn thẳng DH và AH
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
( sử dụng thước vẽ lại cho chính xác nhé. )
a. xét tam giác HBA và tam giác CDB, ta có :
góc B là góc chung ( gt )
góc H = góc D = 90 độ
do đó : tam giác HBA đồng dạng tam giác CDB ( g - g )
b.
• AD/DB = DH/BC
mà BC = AD ( vì ABCD là hcn )
nên AD/BD = DH/AD
= AD . AD = DB . DH
=> AD^2 = DB . DH ( đpcm )
• vì AB = DC ( ABCD là hcn )
nên DC = 8 cm
áp dụng định lý pytago trong tam giác DBC vuông tại C, ta có:
DB^2 = BC^2 + CD^2
DB^2 = 8^2 + 6^2
DB^2 = 64 + 36
DB^2 = 100
DB = căn bậc 2 của 100
DB = 10 ( cm )
vậy DB = 10 cm
Vẽ kèm trục số giúp mình luôn ạ, mình cảm ơn nhiều