§3. Tích của vectơ với một số

20:

a: 5JB=2JC

=>JB/2=JC/5

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{JC}{5}=\dfrac{JB}{2}=\dfrac{JC-JB}{5-2}=\dfrac{BC}{3}\)

=>JC=5/3*BC; JB=2/3BC

2CI=3BI

=>CI/3=BI/2=(CI+BI)/(3+2)=CB/5

=>CI=3/5CB; BI=2/5CB

\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}\)

=\(\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BC}\)

\(=\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}=\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}\)

\(\overrightarrow{AJ}=\overrightarrow{AB}+\overrightarrow{BJ}\)

\(=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{BC}\)

\(=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{BA}-\dfrac{2}{3}\overrightarrow{AC}\)

\(=\dfrac{5}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\)

b: Gọi giao của AG với BC là M

=>M là trung điểm của BC

Xét ΔABC có

G là trọng tâm

AM là đường trung tuyến

=>\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{2}{3}\cdot\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

Đặt \(\overrightarrow{AG}=x\cdot\overrightarrow{AI}+y\cdot\overrightarrow{AJ}\)

=>\(\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{3}{5}\cdot x\cdot\overrightarrow{AB}+\dfrac{2}{5}\cdot x\cdot\overrightarrow{AC}+\dfrac{5}{3}\cdot y\cdot\overrightarrow{AB}-\dfrac{2}{3}\cdot y\cdot\overrightarrow{AC}\)

Đồng nhất hệ số, ta được hệ phương trình:

3/5x+5/3y=1/3 và 2/5x-2/3y=1/3

=>x=35/48 và y=-1/16

=>\(\overrightarrow{AG}=\dfrac{35}{48}\overrightarrow{AI}-\dfrac{1}{16}\overrightarrow{AJ}\)

22:

a:

\(\overrightarrow{AD}=2\overrightarrow{DB}\)

=>\(\overrightarrow{AD}=\dfrac{2}{3}\overrightarrow{AB}\)

\(\overrightarrow{CE}=3\overrightarrow{EA}\)

=>\(\overrightarrow{AE}=\dfrac{1}{3}\overrightarrow{EC}\)

=>\(\overrightarrow{AE}=\dfrac{1}{4}\overrightarrow{AC}\)

Xét ΔAED có AM là trung tuyến

nên \(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AE}\right)\)

\(=\dfrac{1}{2}\left(\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}\)

b: \(\overrightarrow{MI}=\overrightarrow{ME}+\overrightarrow{EI}\)

\(=\dfrac{1}{2}\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CI}\)

\(=\dfrac{1}{2}\left(\overrightarrow{DA}+\overrightarrow{AE}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}\)

\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AB}\)

\(=\dfrac{-1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AB}\)

\(=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)

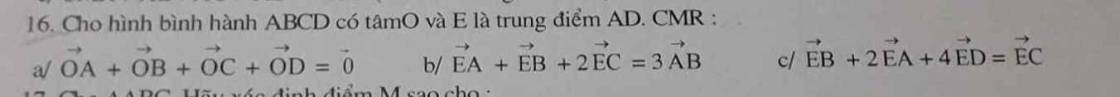
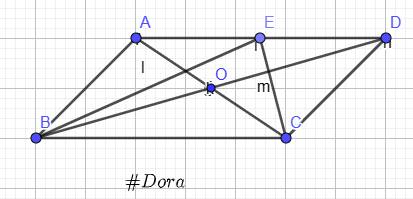
`a)` Vì `O` là trung điểm của `AC;BD`

    `=>{(\vec{OA}=-\vec{OC}),(\vec{OB}=-\vec{OD}):}`

Ta có: `\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}`

    `=-\vec{OC}-\vec{OD}+\vec{OC}+\vec{OD}=0`

`b)` Vì `E` là trung điểm `AD=>\vec{EA}=-\vec{ED}`

Ta có: `\vec{EA}+\vec{EB}+2\vec{EC}`

`=\vec{EA}+\vec{EA}+\vec{AB}+2\vec{ED}+2\vec{DC}`

`=-2\vec{ED}+\vec{AB}+2\vec{ED}+2\vec{AB}=3\vec{AB}`

`c)` Ta có: `\vec{EB}+2\vec{EA}+4\vec{ED}`

`=\vec{EB}-2\vec{ED}+4\vec{ED}`

`=\vec{EB}+2\vec{ED}`

`=\vec{EA}+\vec{AB}+2\vec{ED}`

`=-\vec{ED}+\vec{AB}+2\vec{ED}`

`=\vec{AB}+\vec{EC}+\vec{CD}` (Mà `\vec{AB}=-\vec{CD}`)

`=\vec{EC}`

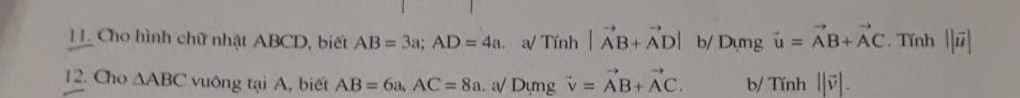
11:

a: ABCD là hình chữ nhật

=>vecto AB+vecto AD=vecto AC

\(AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)

\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC=5a\)

b: Gọi M là trung điểm của BC

=>BM=MC=4a/2=2a

Trên tia đối của tia MA lấy D sao cho M là trung điểm của AD

Xét tứ giác ABDC có

M là trung điểm chung của AD và BC

=>ABDC là hình bình hành

=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}=2\cdot\overrightarrow{AM}\)

\(AM=\sqrt{AB^2+BM^2}=\sqrt{\left(3a\right)^2+\left(2a\right)^2}=a\sqrt{13}\)

=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)

12:

a: Gọi M là trung điểm của BC

trên tia đối của tia MA, lấy D sao cho M là trung điểm của AD

Xét tứ giác ABDC có

M là trung điểm chung của AD và BC

góc BAC=90 độ

=>ABDC là hình chữ nhật

=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)

=>\(\overrightarrow{v}=\overrightarrow{AD}\)

b: \(\left|\overrightarrow{v}\right|=\left|\overrightarrow{AD}\right|=AD=2\cdot AM=2\cdot\dfrac{BC}{2}=BC=\sqrt{\left(6a\right)^2+\left(8a\right)^2}=10a\)

11:

a: \(BD=AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)

|vecto AB+vecto AD|

=|vecto AB+vecto BC|

=|vecto AC|

=5a

b: Gọi M là trung điểm của BC

=>BM=CM=BC/2=2a

\(AM=\sqrt{AB^2+BM^2}=a\sqrt{13}\)

Xét ΔABC có AM là trung tuyến

nên vecto AB+vecto AC=2*vecto AM

=>|vecto AB+vecto AC|=2|vecto AM|

=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)

Đề có phải là: \(\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{0}\) 

Gọi I là trung điểm AB

(Chèn điểm) \(\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}=\overrightarrow{MC}\)

\(\Leftrightarrow2\overrightarrow{MI}=\overrightarrow{MC}\)

Suy ra M nằm trên đường thẳng IC với I là trung điểm của MC