Bài 5: 

a: Xét ΔBEC và ΔADC có 

\(\widehat{C}\) chung

\(\widehat{EBC}=\widehat{DAC}\)

Do đó: ΔBEC\(\sim\)ΔADC

1 was given

2 have repaired

3 had finished

4 isn't reading

5 had talked

1 was found

2 are always

8 ko có từ

9 have become

10 had met

11 aren't

12 arrives

13 is repairing

14 was built

15 had finished

16 will stay

Bài 1: 

a: =3x(x+2)

b: \(=x\left(x-1\right)^2\)

c: \(=x^2\left(x-y\right)-\left(x-y\right)=\left(x-y\right)\left(x-1\right)\left(x+1\right)\)

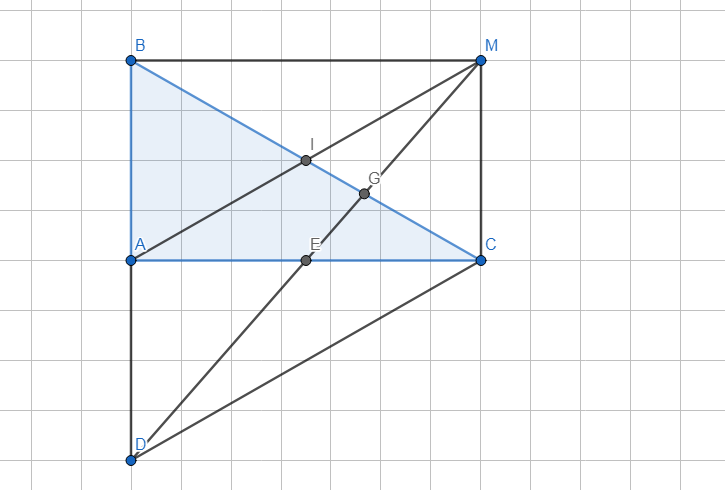
Bài 4:

b) Xét tứ giác AMCD có:

AD//CM (ABMC là hình chữ nhật).

AD=AB=CM (D là điểm đối đứng với B qua A, ABMC là hình chữ nhật).

=> AMCD là hình bình hành.

\(a-b=2\Leftrightarrow a=b+2\)

\(P=3a^2+b^2+8\\ P=3\left(b+2\right)^2+b^2+8\\ P=3b^2+12b+12+b^2+8\\ P=4b^2+12b+20\\ P=\left(4b^2+12b+9\right)+11\\ P=\left(2b+3\right)^2+11\ge11\forall a;b\)

Dấu "=" xảy ra \(\Leftrightarrow b=\dfrac{-3}{2}\)

Pmin = 11

a: Ta có: EC//AB

AB⊥CD

Do đó: EC⊥CD

=>ΔCED nội tiếp đường tròn đường kính CD

=>O là trung điểm của CD(Vì C,E,D cùng nằm trên đường tròn O)

=>E,O,D thẳng hàng

b: Xét (O) có

ΔAEB nội tiếp

AB là đường kính

DO đó: ΔAEB vuông tại E

Xét tứ giác AEBD có 

O là trung điểm của AB

O là trung điểm của ED

Do đó: AEBD là hình bình hành

mà \(\widehat{AEB}=90^0\)

nên AEBD là hình chữ nhật

\(A=\sqrt{2a\left(b+1\right)}+\sqrt{2b\left(c+1\right)}+\sqrt{2c\left(a+1\right)}\)

\(A=\dfrac{1}{\sqrt{2}}\sqrt{4a\left(b+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4b\left(c+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4c\left(a+1\right)}\)

\(A\le\dfrac{1}{2\sqrt{2}}\left(4a+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4b+c+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+a+1\right)\)

\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)

\(A_{max}=2\sqrt{2}\) khi \(a=b=c=\dfrac{1}{3}\)