\(cos^23x.cos2x-cos^2x=0\)
Tìm x
1)\(sin^23x.cos2x+sin^2x=0\)
2)
\(cos^23x+cos^22x=sin^2x\)
3)
\(\frac{1}{4}+cos^2\frac{x}{3}=\frac{1}{2}sin^2\frac{x}{2}\)
4)
\(sin^23x-sin^22x-sin^2x=0\)
5)
\(2cos^2x=3sin^25x+2\)
6) 3cosx+2cos2x-cos3x=2sinxsin2x-1
7) \(sinx+cosx=\sqrt{2}\left(2-sin^32x\right)\)
1.
\(\Leftrightarrow\left(1-cos6x\right)cos2x+1-cos2x=0\)
\(\Leftrightarrow cos2x-cos2x.cos6x+1-cos2x=0\)
\(\Leftrightarrow\frac{1}{2}\left(cos8x-cos4x\right)-1=0\)
\(\Leftrightarrow2cos^24x-cos4x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=-1\\cos4x=\frac{3}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow4x=\pi+k2\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
2.
\(\Leftrightarrow1+cos6x+2cos^22x=1-cos2x\)
\(\Leftrightarrow cos6x+cos2x+2cos^22x=0\)
\(\Leftrightarrow cos4x.cos2x+cos^22x=0\)
\(\Leftrightarrow cos2x\left(cos4x+cos2x\right)=0\)
\(\Leftrightarrow cos2x\left(2cos^22x+cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=-1\\cos2x=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\frac{\pi}{2}+k\pi\\x=\pm\frac{\pi}{6}+k\pi\end{matrix}\right.\)
3.
Đặt \(\frac{x}{6}=t\Rightarrow\frac{1}{4}+cos^22t=\frac{1}{2}sin^23t\)
\(\Leftrightarrow1+4cos^22t=1-cos6t\)
\(\Leftrightarrow cos6t+4cos^22t=0\)
\(\Leftrightarrow4cos^32t+4cos^22t-3cos2t=0\)
\(\Leftrightarrow cos2t\left(4cos^22t+4cos2t-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2t=0\\cos2t=\frac{1}{2}\\cos2t=-\frac{3}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\frac{\pi}{4}+\frac{k\pi}{2}\\t=\pm\frac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{x}{3}=\frac{\pi}{4}+\frac{k\pi}{2}\\\frac{x}{3}=\frac{\pi}{6}+k\pi\\\frac{x}{3}=-\frac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow x=...\)
Tìm góc α ∈ π 6 ; π 4 ; π 3 ; π 2 để phương trình cos 2 x + 3 sin 2 x - 2 cos x = 0 tương đương với phương trình cos ( 2 x - α ) = cos x
![]()
![]()
![]()
![]()
Đáp án D
Ta có
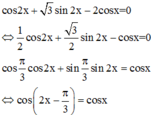
Do đó để phương trình ![]() tương đương với phương trình
tương đương với phương trình
![]()
Tìm góc α ∈ π 6 ; π 4 ; π 3 ; π 2 để phương trình cos 2 x + 3 sin 2 x - 2 cos x = 0 tương đương với phương trình cos ( 2 x - α ) = cos x
![]()
![]()
![]()
![]()
Đáp án D
Dùng công thức cos a.cos b+ sin a. sin b= cos (a-b) để biến đổi phương trình không chứa
α
về dạng giống phương trình có chứa
α
Ta có
Tìm số nghiệm của phương trình cos 2x - cos x - 2 = 0, x ∈ 0 , 2 π
A. 0
B. 2
C. 1
D. 3
1. Tìm m để PT có nghiệm:
a) \(\sqrt{3}\cos^2x+\dfrac{1}{2}\sin2x=m\)
b) \(3\sin^2x-2\sin x\cos x+m=0\)
c) \(\sin^2x+2\left(m-1\right)\sin x\cos x-\left(m+1\right)\cos^2x=m\)
b.
\(\Leftrightarrow\dfrac{3}{2}\left(1-cos2x\right)-sin2x+m=0\)
\(\Leftrightarrow sin2x+\dfrac{3}{2}cos2x-\dfrac{3}{2}=m\)
\(\Leftrightarrow\dfrac{\sqrt{13}}{2}\left(\dfrac{2}{\sqrt{13}}sin2x+\dfrac{3}{\sqrt{13}}cos2x\right)-\dfrac{3}{2}=m\)
Đặt \(\dfrac{2}{\sqrt{13}}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\dfrac{\sqrt{13}}{2}sin\left(2x+a\right)-\dfrac{3}{2}=m\)
Phương trình có nghiệm khi và chỉ khi:
\(\dfrac{-\sqrt{13}-3}{2}\le m\le\dfrac{\sqrt{13}-3}{2}\)
Lý thuyết đồ thị:
Phương trình \(f\left(x\right)=m\) có nghiệm khi và chỉ khi \(f\left(x\right)_{min}\le m\le f\left(x\right)_{max}\)
Hoặc sử dụng điều kiện có nghiệm của pt lương giác bậc nhất (tùy bạn)
a.
\(\dfrac{\sqrt{3}}{2}\left(1-cos2x\right)+\dfrac{1}{2}sin2x=m\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x+\dfrac{\sqrt{3}}{2}=m\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)+\dfrac{\sqrt{3}}{2}=m\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi:
\(-1+\dfrac{\sqrt{3}}{2}\le m\le1+\dfrac{\sqrt{3}}{2}\)
c.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos2x+\left(m-1\right)sin2x-\left(m+1\right)\left(\dfrac{1}{2}+\dfrac{1}{2}cos2x\right)=m\)
\(\Leftrightarrow\left(2m-2\right)sin2x-\left(m+2\right)cos2x=3m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt có nghiệm khi:
\(\left(2m-2\right)^2+\left(m+2\right)^2\ge9m^2\)
\(\Leftrightarrow m^2+m-2\le0\)
\(\Leftrightarrow-2\le m\le\)
1. Tìm m để PT có nghiệm:
a) \(\sqrt{3}\cos^2x+\dfrac{1}{2}\sin2x=m\)
b) \(3\sin^2x-2\sin x\cos x+m=0\)
c) \(^{ }\sin^2x+2\left(m-1\right)\sin x\cos x-\left(m+1\right)\cos^2x=m\)
a) \(\sqrt{3}\left(\dfrac{1+cos2x}{2}\right)+\dfrac{1}{2}sin2x=m\) ↔ \(\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x=m-\dfrac{\sqrt{3}}{2}\)
→\(\sqrt{3}cos2x+sin2x=2m-\sqrt{3}\) ↔ \(2cos\left(\dfrac{\pi}{6}-2x\right)=2m-\sqrt{3}\)
→\(cos\left(\dfrac{\pi}{6}-2x\right)=m-\dfrac{\sqrt{3}}{2}\)
Pt có nghiệm khi và chỉ khi \(-1\le m-\dfrac{\sqrt{3}}{2}\le1\)
b) \(\left(3+m\right)sin^2x-2sinx.cosx+mcos^2x=0\)
cosx=0→ sinx=0=> vô lý
→ sinx#0 chia cả 2 vế của pt cho cos2x ta đc:
\(\left(3+m\right)tan^2x-2tanx+m=0\)
pt có nghiệm ⇔ △' ≥0
Tự giải phần sau
c) \(\left(1-m\right)sin^2x+2\left(m-1\right)sinx.cosx-\left(2m+1\right)cos^2x=0\)
⇔cosx=0→sinx=0→ vô lý
⇒ cosx#0 chia cả 2 vế pt cho cos2x
\(\left(1-m\right)tan^2x+2\left(m-1\right)tanx-\left(2m+1\right)=0\)
pt có nghiệm khi và chỉ khi △' ≥ 0
Tự giải
Giải các pt sau:
a) \(\cos^2x-\cos x=0\)
b) \(2\sin2x\) + \(\sqrt{2}\sin4x=0\)
c) \(8\cos^2x+2\sin x-7=0\)
d) \(4\cos^4x+\cos^2x-3=0\)
e) \(\sqrt{3}\tan x-6\cot x+\left(2\sqrt{3}-3\right)=0\)
a, \(cos^2x-cosx=0\)
\(\Leftrightarrow cosx\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=0\end{matrix}\right.\)
b, \(2sin2x+\sqrt{2}sin4x=0\)
\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\1+\sqrt{2}cos2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\cos2x=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\2x=\dfrac{3\pi}{4}+k2\pi\\2x=\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{3\pi}{8}+k\pi\\x=\dfrac{\pi}{8}+k\pi\end{matrix}\right.\)
a, \(cos^2x-cosx=0\)
\(\Leftrightarrow cosx\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=k2\pi\end{matrix}\right.\) (k ∈ Z)
Vậy...
b, \(2sin2x+\sqrt{2}sin4x=0\)
\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow2sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\cos2x=\dfrac{-\sqrt{2}}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\2x=\pm\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\pm\dfrac{3\pi}{8}+k\pi\end{matrix}\right.\)
Vậy...
c, \(8cos^2x+2sinx-7=0\)
\(\Leftrightarrow8\left(1-sin^2x\right)+2sinx-7=0\)
\(\Leftrightarrow8sin^2x-2sinx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=-\dfrac{1}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\x=arcsin\left(-\dfrac{1}{4}\right)+k2\pi\\x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k2\pi\end{matrix}\right.\)
Vậy...
d, \(4cos^4x+cos^2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^2x=\dfrac{3}{4}\\cos^2x=-1\left(loai\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{cos2x+1}{2}=\dfrac{3}{4}\)
\(\Leftrightarrow cos2x=\dfrac{1}{2}\)
\(\Leftrightarrow2x=\pm\dfrac{\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+k\pi\)
Vậy...
e, \(\sqrt{3}tanx-6cotx+\left(2\sqrt{3}-3\right)=0\) (ĐK: \(x\ne\dfrac{k\pi}{2}\))
\(\Leftrightarrow\sqrt{3}tanx-\dfrac{6}{tanx}+\left(2\sqrt{3}-3\right)=0\)
\(\Leftrightarrow\sqrt{3}tan^2x+\left(2\sqrt{3}-3\right)tanx-6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\left(tm\right)\\x=arctan\left(-2\right)+k\pi\end{matrix}\right.\)
Vậy...
c, \(8cos^2x+2sinx-7=0\)
\(\Leftrightarrow-8sin^2x+2sinx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=-\dfrac{1}{4}\end{matrix}\right.\)
Với \(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Với \(sinx=-\dfrac{1}{4}\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(-\dfrac{1}{4}\right)+k2\pi\\x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k2\pi\end{matrix}\right.\)
d, \(4cos^4x+cos^2x-3=0\)
\(\Leftrightarrow\left(4cos^2x-3\right)\left(cos^2x+1\right)=0\)
\(\Leftrightarrow4cos^2x-3=0\left(\text{Vì }cos^2x+1>0\right)\)
\(\Leftrightarrow cos^2x=\dfrac{3}{4}\)
\(\Leftrightarrow cosx=\pm\dfrac{\sqrt{3}}{2}\)
Với \(cosx=\dfrac{\sqrt{3}}{2}\Leftrightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)
Với \(cosx=-\dfrac{\sqrt{3}}{2}\Leftrightarrow x=\pm\dfrac{5\pi}{6}+k2\pi\)
22. Tìm nghiệm dương nhỏ nhất của PT: \(3\sin^2x+2\sin x\cos x-\cos^2x=0\)
23. Giải PT: \(\sqrt{3}\cos x+2\sin^2\left(\dfrac{x}{2}-\dfrac{\pi}{1}\right)=1\)
\(\sqrt{3}cosx+2sin^2\left(\dfrac{x}{2}-\pi\right)=1\)
\(\Leftrightarrow\sqrt{3}cosx+2sin^2\dfrac{x}{2}=1\)
\(\Leftrightarrow\sqrt{3}cosx-cosx=0\Leftrightarrow cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\) ( k thuộc Z )
Vậy ...
22.
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(3tan^2x+2tanx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất của pt là: \(x=arctan\left(\dfrac{1}{3}\right)\)
22. PT đã cho tương đương
3 - 4cos2x + 2 sinxcosx = 0
⇔ 3 - 2 - 2cos2x + sin2x = 0
⇔ 1 - 2cos2x + sin2x = 0
⇔ 1 + sin2x = 2cos2x
⇔ sin\(\dfrac{\pi}{2}\) + sin2x = 2cos2x
⇔ \(2sin\left(\dfrac{\pi}{4}+x\right).cos\left(\dfrac{\pi}{4}-x\right)\) = 2cos2x
Do \(\left(\dfrac{\pi}{4}-x\right)+\left(\dfrac{\pi}{4}+x\right)=\dfrac{\pi}{2}\)
⇒ \(sin\left(\dfrac{\pi}{4}+x\right)=cos\left(\dfrac{\pi}{4}-x\right)\)
Vậy sin2\(\left(x+\dfrac{\pi}{4}\right)\) = cos2x
Cái này là hiển nhiên ????
Tìm số đo góc nhọn x:
a) \(4\sin x-1=1\)
b) \(2\sqrt{3}-3\tan x=\sqrt{3}\)
c) \(7\sin-3\cos\left(90^o-x\right)=2,5\)
d) \(\left(2\sin-\sqrt{2}\right)\left(4\cos-5\right)=0\)
e) \(\dfrac{1}{\cos^2x}-\tan x=1\)
f) \(\cos^2x-3\sin^2x=0,19\)
a) \(4sinx-1=1\Leftrightarrow4sinx=2\Leftrightarrow sinx=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow x=30^o\)
b) \(2\sqrt{3}-3tanx=\sqrt{3}\Leftrightarrow3tanx=2\sqrt{3}-\sqrt{3}=\sqrt{3}\Leftrightarrow tanx=\dfrac{\sqrt{3}}{3}\)
\(\Leftrightarrow x=30^o\)
c) \(7sinx-3cos\left(90^o-x\right)=2,5\Leftrightarrow7sinx-3sinx=2,5\Leftrightarrow4sinx=2,5\Leftrightarrow sinx=\dfrac{5}{8}\Leftrightarrow x=30^o41'\)
d)\(\left(2sin-\sqrt{2}\right)\left(4cos-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2sin-\sqrt{2}=0\\4cos-5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}2sin=\sqrt{2}\\4cos=5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}sin=\dfrac{\sqrt{2}}{2}\\cos=\dfrac{5}{4}\left(loai\right)\end{matrix}\right.\)\(\Rightarrow x=45^o\)
Xin lỗi nãy đang làm thì bấm gửi, quên còn câu e, f nữa:"(
e) \(\dfrac{1}{cos^2x}-tanx=1\Leftrightarrow1+tan^2x-tanx-1=0\Leftrightarrow tan^2x-tanx=0\Leftrightarrow tanx\left(tanx-1\right)=0\Rightarrow tanx-1=0\Leftrightarrow tanx=1\Leftrightarrow x=45^o\)
f) \(cos^2x-3sin^2x=0,19\Leftrightarrow1-sin^2x-3sin^2x=0,19\Leftrightarrow1-4sin^2x=0,19\Leftrightarrow4sin^2x=0,81\Leftrightarrow sin^2x=\dfrac{81}{400}\Leftrightarrow sinx=\dfrac{9}{20}\Leftrightarrow x=26^o44'\)