CHO HÌNH VẼ CHỨNG MINH a// b// c
Cho hình vẽ sau:
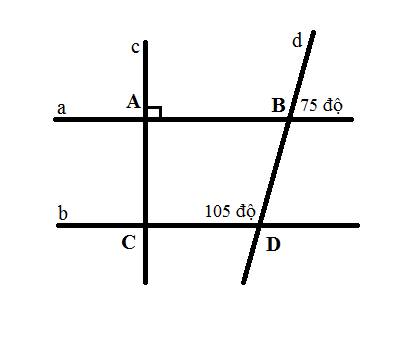
a) Tính số đo góc ABD?
b) Chứng minh a//b
c) Chứng minh \(c\perp b\)
a) Do \(\widehat{ABD}\) đổi đỉnh với góc bên ngoài
\(\Rightarrow\widehat{ABD}=75^o\)
b) Ta có \(\widehat{ABd}=180^o-75^o=105^o\) (kể bù)
\(\Rightarrow\widehat{\text{C}DB}=\widehat{ABd}=105^o\)
Mà hai góc này ở vị trí đồng vị
\(\Rightarrow a//b\)
d) Ta có: \(a//b\) và \(a\perp c\)
\(\Rightarrow b\perp c\)
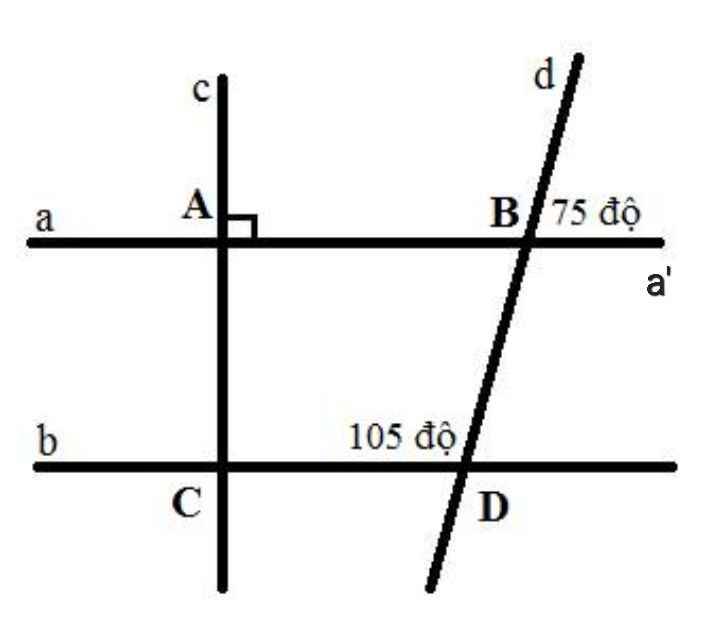 a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
⇒ ∠ABD = ∠dBa' = 75⁰
b) Ta có:
∠ABD + ∠a'BD = 180⁰ (kề bù)
⇒ ∠a'BD = 180⁰ - ∠ABD
= 180⁰ - 75⁰
= 105⁰
⇒ ∠a'BD = ∠CDB = 105⁰
Mà ∠a'BD và ∠CDB là hai góc so le trong
⇒ a // b
c) Do c ⊥ a (gt)
a // b (cmt)
⇒ c ⊥ b
Cho hình vẽ bên: a) Chứng minh: tam giác OCB = tam gíác ODE
b) Chứng minh: góc B = góc E
c) Chứng minh: BC // DE ![]()
a: Xét ΔOCB và ΔODE có
OC=OD
CB=DE
OB=OE
Do đó: ΔOCB=ΔODE
Học sinh vẽ lại hình, viết giả thiết kết luận và trình bày lời giải bài toán sau: Cho hình vẽ bên Biết b vuông góc c; 𝐴̂1 = 550; 𝐵̂1 = 550𝐶̂1 = 1200a) Chứng minh: a //b b) Chứng minh: a vuông góc c c) Tính số đo 𝐵𝑂𝐶 ̂
vì c cắt a và b tạo thành cặp vuông góc bằng nha
⇒ a//b
à nhớ chứng minh là AB cắt a và b taoh thành cặp góc đồng vị bằng nhau
cho hình vẽ
Biết AB//CD
AB=CD
A) chứng minh ΔABC=ΔCDB
B) chứng minh AD=BC
C) chứng minh AD//BC
b: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó:ABCD là hình bình hành
Suy ra: AD=BC
cho hình vẽ biết B=A+C chứng minh Ax // Cy
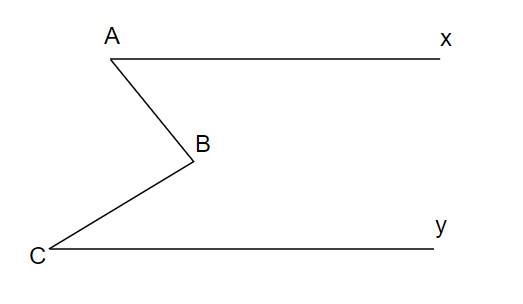
Kéo dài AB cắt Cy tại E và kéo dài CB cắt Ax tại G như hình vẽ dưới đây:
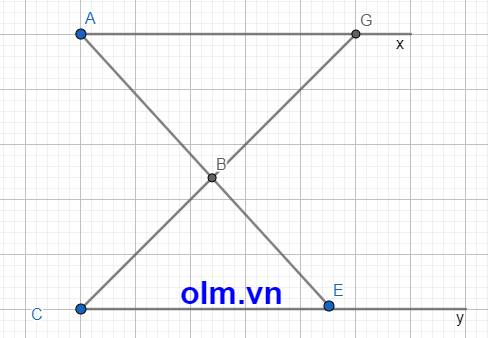
\(\widehat{ABC}\) = \(\widehat{GBE}\) (1) (vì đối đỉnh)
\(\widehat{GBE}\) = \(\widehat{BCE}\) + \(\widehat{CEB}\) (2) ( vì góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{ABC}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\) (3)
Từ (1); (2); (3) ta có: \(\widehat{BCE}\) + \(\widehat{CEB}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\)
⇒ \(\widehat{CEB}\) = \(\widehat{GAB}\)
Mà hai góc CEB và góc GAB là hai góc ở vị trí so le trong nên
Cy // Ax (đpcm)
Cho hình vẽ sau. Chứng minh A1 + ACM = B1 + BMC
Mình bổ sung thêm là a vuông góc với c nha
Cho hình vẽ, chứng minh rằng :
a//c, b//c
Lời giải:
Ta thấy:
$\widehat{aAb}=120^0=\widehat{cBA}$. Mà hai góc này ở vị trí so le trong nên $Aa\parallel Cb$ (đpcm)
Kẻ tia $Bc'$ là tia đối của tia $Bc$
Khi đó:
$\widehat{cBA}+\widehat{ABc'}=180^0$
$120^0+\widehat{ABc'}=180^0$
$\widehat{ABc'}=60^0$
$\widehat{c'Bc}=\widehat{ABC}-\widehat{ABc'}=80^0-60^0=20^0$
$\widehat{c'Bc}+\widehat{BCb}=20^0+160^0=180^0$ mà 2 góc này ở vị trí trong cùng phía nên $Bc'\parallel Cb$
Mà $Bc', Bc$ là 2 tia đối nên $Cb\parallel cB$ (đpcm)
Bài 1: Cho hình vẽ D=60; C=120
Chứng minh AB vuông góc với b
Bài 2: Cho hình vẽ
Chứng tỏ a//b//c
Các bạn giúp mình nhé, cảm ơn rất nhiều
Bài 2: ta thấy A và B ở vị trí trong cùng phía , A + B = 180 độ =>a//b(1)
Ta lại thấy B , C ở vị trí đồng vị , B=C=70 độ =>b//c(2)
Từ 1,2 =>a//b//c
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz

a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
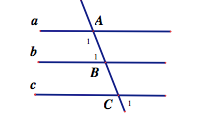
Cho hình vẽ. Biết A1 + B1 = 180độ , B1 = C1. Chứng minh rằng A//B//C ?
\(\hat{A}_1+\hat{B}_1=180^o\Rightarrow a\text{ // }b\left(tcp\right)\)
\(\hat{B}_1=\hat{C}_1\Rightarrow b\text{ // }c\left(đv\right)\)
\(\Rightarrow a\text{ // }b\text{ // }c\left(đpcm\right)\)