Tâm của đường tròn qua ba điểm A(2;1), B(2;5), C(-2;1) thuộc đường thẳng có phương trình?
help mee
HY
Những câu hỏi liên quan
Cho nửa đường tròn tâm O đường kính BC = 2R và 1 điểm A trên nửa đường tròn đó.Vẽ AH vuông góc với BC. Gọi I và K lần lượt là các điểm đối xứng của H qua AB và qua AC.Chứng minh rằng
a) Ba điểm I,A,K thẳng hàng
b) IK là tiếp tuyến của đường tròn tâm O
Cho nửa đường tròn tâm O đường kính BC = 2R và 1 điểm A trên nửa đường tròn đó.Vẽ AH vuông góc với BC. Gọi I và K lần lượt là các điểm đối xứng của H qua AB và qua AC.Chứng minh rằng
a) Ba điểm I,A,K thẳng hàng
b) IK là tiếp tuyến của đường tròn tâm O
Câu 27. Xét các khẳng định trong đây khẳng định nào sai:
(I) Tâm của đường tròn là tâm đối xứng của đường tròn đó.
(II) Qua hai điểm ta vẽ được một đường tròn.
(III) Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
(IV) Qua ba điểm không thẳng hàng ta vẽ được vô số đường tròn.
Số khẳng định đúng là
Câu 27. Xét các khẳng định sau:
(I) Tâm của đường tròn là tâm đối xứng của đường tròn đó.
(II) Qua hai điểm ta vẽ được một đường tròn.
(III) Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
(IV) Qua ba điểm không thẳng hàng ta vẽ được vô số đường tròn.
Số khẳng định đúng là
Câu 27. Xét các khẳng định sau:(I) Tâm của đường tròn là tâm đối xứng của đường tròn đó.(II) Qua hai điểm ta vẽ được một đường tròn. (III) Bất kì đường kính nào cũng là trục đối xứng của đường tròn. (IV) Qua ba điểm không thẳng hàng ta vẽ được vô số đường tròn. Số khẳng định đúng là A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Câu 27. Xét các khẳng định sau:
(I) Tâm của đường tròn là tâm đối xứng của đường tròn đó.
(II) Qua hai điểm ta vẽ được một đường tròn.
(III) Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
(IV) Qua ba điểm không thẳng hàng ta vẽ được vô số đường tròn.
Số khẳng định đúng là
A. 1 B. 2 C. 3 D. 4
Tâm của đường tròn qua ba điểm A( 2;1) ; B( 2;5) và C( -2;1) thuộc đường thẳng có phương trình A. x- y+ 3 0. B. x+ y-3 0 C. x-y-3 0 D. x+ y+ 3 0
Đọc tiếp
Tâm của đường tròn qua ba điểm A( 2;1) ; B( 2;5) và C( -2;1) thuộc đường thẳng có phương trình
A. x- y+ 3= 0.
B. x+ y-3= 0
C. x-y-3 = 0
D. x+ y+ 3= 0
Phương trình đường tròn (C) có dạng:
x2 + y2 -2ax – 2by + c= 0 ( a2+ b2 –c > 0)
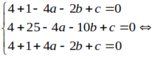
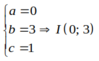
Vậy tâm đường tròn là I( 0;3) .
Lần lượt thay tọa độ I vào các phương trình đường thẳng thì chỉ có đường thẳng x- y+ 3= 0 thỏa mãn.
Chọn A.
Đúng 0
Bình luận (0)
Cho đường tròn tâm O và dây AB cố định, điểm M tùy ý thay đổi trên đoạn AB. Qua A và M dựng đường tròn tâm I tiếp xúc đường tròn tâm O tại A. Qua B và M dựng đường tròn tâm J tiếp xúc đường tròn tâm O tại B. 2 đường tròn tâm I và đường tròn tâm J cắt nhau tại điểm thứ 2 là N. CMR MN luôn đi qua 1 điểm cố định
Cho đường tròn tâm o,R và đường thẳng d không qua O cắt đường tròn tại hai điểm A,B.Lấy 1 điểm M trên tia đối của tia BA kẻ 2 tiếp tuyến MC MD với đường tròn C,D là tiếp điểm H là trung điểm AB
a CM MDOH nội tiếp
b OM cắt đường tròn tại I CM I là tâm đường tròn nội tiếp MCD
Cho tam giác ABCvuông tại A. Gọi M,N,P lần lượt là trung điểm của BC,CA,AB. Xác định tâm O đường tròn đi qua ba điểm M,N,P. Đường tròn này còn đi qua điểm nào khác?
Cho ba điểm A,B,C cố định thẳng hàng theo thứ tự đó. Đường tròn tâm O di động luôn đi qua B, C. kẻ qua A các tiếp tuyến AE, AF đến đường tròn tâm O. Gọi E,F là hai tiếp điểm . Gọi I là trung điểm của BC và K là giao của FI với đường tròn tâm O. CMR: véc tơ EK và véc tơ AB cùng phương
a) Vì tam giác AFB đồng dạng với ACF(g.g) nên:
AF/AC=AB/AF hay AF^2=AB.AC => AF=căn(AB.AC) ko đổi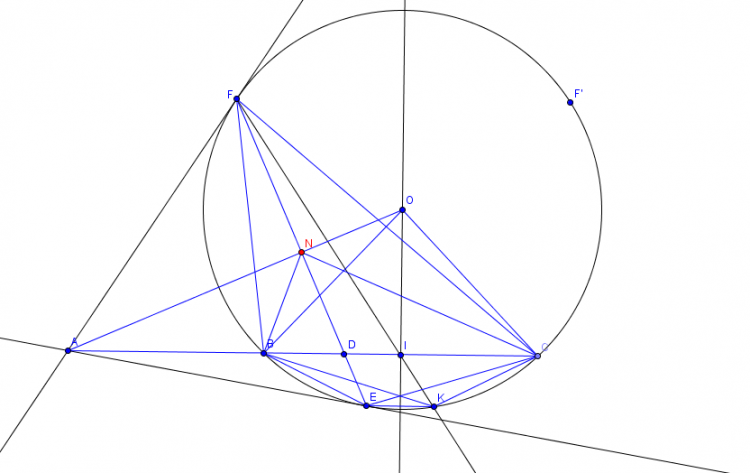 
Mà AE=AF (T/cTtuyen) nên E, F cùng thuộc đường tròn bán kính căn(AB.AC)
b)Ta có: OI vuông góc với BC (T/ đường kính và dây)
Các điểm E, F, I cùng nhìn OA dưới 1 góc ko đổi 90 độ nên O,I,F,A,E cùng thuộc đường tròn đường kính OA
Ta có góc FIA=FOA(Cùng chắn cung FA trong đường tròn (OIFAE)
Mà góc FKE=FOA( Cùng bằng \(\frac{1}{2}\) góc FOE)
Suy ra góc FIA=FKE, nhưng hai góc này lại ở vị trí SLT nên KE//AB
Đúng 0
Bình luận (1)