Nhầm xíu, quên không khai căn, thế này mới đúng :D

\(y=\dfrac{\sqrt{26}}{5}\left(\dfrac{5\sqrt{26}}{26}sinx+\dfrac{\sqrt{26}}{26}cosx\right)=\dfrac{\sqrt{26}}{5}sin\left(x+\alpha\right)\)

Với \(\alpha=arccos\dfrac{5\sqrt{26}}{26}\)

Do \(-1\le sin\left(x+\alpha\right)\le1\Rightarrow\dfrac{-\sqrt{26}}{5}\le y\le\dfrac{\sqrt{26}}{5}\)

\(\Rightarrow\left\{{}\begin{matrix}y_{min}=\dfrac{-\sqrt{26}}{5}\\y_{max}=\dfrac{\sqrt{26}}{5}\end{matrix}\right.\)

\(y=\dfrac{26}{25}\left(\dfrac{25}{26}sinx+\dfrac{5}{26}.cosx\right)=\dfrac{26}{25}sin\left(x+\alpha\right)\) với \(\alpha=arccos\dfrac{25}{26}\)

Do \(-1\le sin\left(x+\alpha\right)\le1\) \(\Rightarrow\dfrac{-26}{25}\le y\le\dfrac{26}{25}\)

\(\Rightarrow y_{min}=-\dfrac{26}{25}\) ; \(y_{max}=\dfrac{26}{25}\)

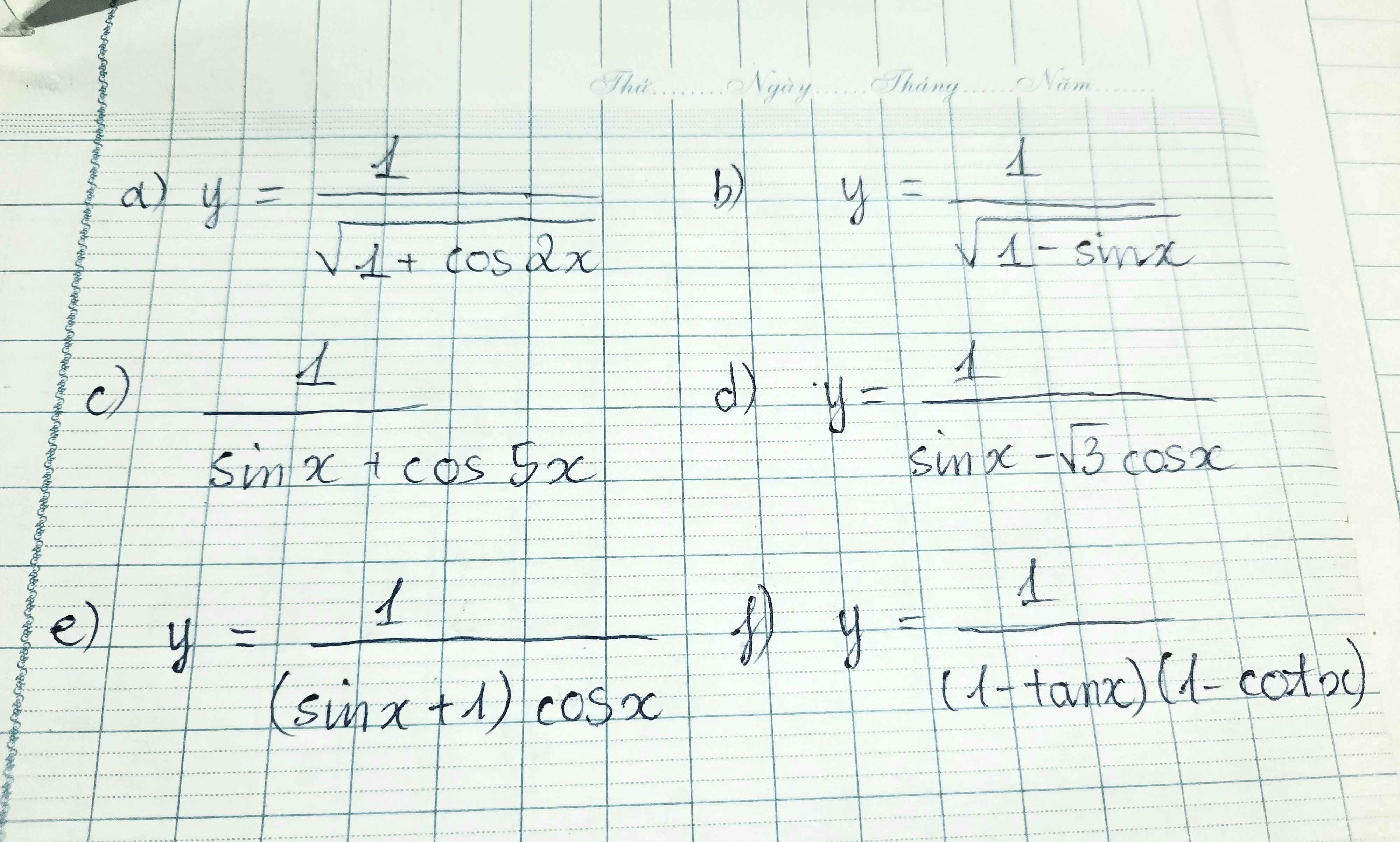
a) Hàm số xđ <=> \(1+cos2x>0\) \(\Leftrightarrow cos2x\ne-1\) \(\Leftrightarrow\)\(2cos^2x-1\ne-1\)

\(\Leftrightarrow cosx\ne0\) \(\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\)

b)Hàm số xđ <=> \(1-sinx>0\) \(\Leftrightarrow sinx\ne1\) \(\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)

c) Hàm số xđ <=> \(sinx+cos5x\ne0\)

\(\Leftrightarrow sinx\ne-cos5x\)

\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-x\right)\ne cos\left(\pi-5x\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\pi}{2}-x\ne\pi-5x+k2\pi\\\dfrac{\pi}{2}-x\ne-\pi+5x+k2\pi\end{matrix}\right.\) (\(k\in Z\))

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{8}+\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}-\dfrac{k\pi}{3}\end{matrix}\right.\)(\(k\in Z\))

d) Hàm số xđ <=> \(sinx-\sqrt{3}cosx\ne0\)

\(\Leftrightarrow2.sin\left(x-\dfrac{\pi}{3}\right)\ne0\) \(\Leftrightarrow x\ne\dfrac{\pi}{3}+k\pi\left(k\in Z\right)\)

e) Hàm số xđ <=> \(\left(sinx+1\right).cosx\ne0\)

\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne-1\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{\pi}{2}+k2\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Rightarrow x\ne\dfrac{\pi}{2}+k\pi\) (Hai họ nghiệm trùng nhau nên e tổng hợp lại, e nghĩ thế)

f) Hàm số xđ <=> \(\left\{{}\begin{matrix}\left(1-tanx\right)\left(1-cotx\right)\ne0\\sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}tanx\ne1\\cotx\ne1\\sinx.cosx\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne cosx\\\dfrac{1}{2}.sin2x\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne sin\left(\dfrac{\pi}{2}-x\right)\\2x\ne k\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}-x+k2\pi\\x\ne\dfrac{\pi}{2}+x+k2\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\))

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\0\ne\dfrac{\pi}{2}+k2\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\)) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\))

giúp đi mà tui cần gấp

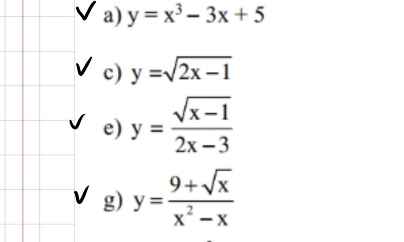
a: TXĐ: D=R

c: TXĐ: D=[1/2;+\(\infty\))

ĐKXĐ:

a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\)  \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)

b. \(D=R\)

c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)

d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)

Hàm là vậy phải không nhỉ? \(y=\dfrac{sin^2x-3sinx}{\left(tanx-1\right)\left(cotx+1\right)}\)

ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\tanx-1\ne0\\cotx+1\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne1\\cotx\ne-1\end{matrix}\right.\) 

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)

\(\Leftrightarrow x\ne\dfrac{k\pi}{4}\)