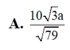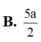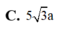Nếu tam giác ABC có \(cosA=-\frac{\sqrt{3}}{2}\) thì góc giữa hai đường thẳng AB và BC là:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB=a , AB vuông góc với SA , BC vuông góc với SC . Gọi M,N lần lượt là trung điểm SC,AC . Góc giữa hai mặt phẳng (BMN) và (SAB) là a thỏa mãn cosa= \(\dfrac{\sqrt{5}}{3}\).Thể tích khối chóp S.BMN bằng bao nhiêu?
Cho lăng trụ tam giác đều ABC.A’B’C’ có bán kính đường tròn ngoại tiếp đáy ABC bằng 2 a 3 3 và góc giữa hai đường thẳng AB’ và BC’ bằng 60 độ Tính khoảng cách giữa hai đường thẳng AB’ và BC’ ?
A. d = 2 a 2 3
B. d = 4a/3
C. d = 2 a 3 3
D. d = 2 a 6 3
Cho hình lăng trụ tam giác đều ABC.A'B'C' có bán kính đường tròn ngoại tiếp đáy ABC bằng 2 a 3 3 và góc giữa hai đường thẳng AB' và BC' bằng 60 o . Tính khoảng cách d giữa hai đường thẳng AB' và BC' ?
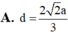
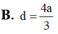
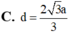
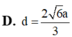
Cho hình lăng trụ tam giác đều ABCD.A'B'C'D' có bán kính đường tròn ngoại tiếp đáy ABC bằng 2 a 3 3 và góc giữa hai đường thẳng AB' và BC' bằng 60 ∘ . Tính khoảng cách d giữa hai đường thẳng AB' và BC' ?
A. d = 2 2 a 3
B. d = 4 a 3
C. d = 2 3 a 3
D. d = 2 6 a 3
Đáp án A

Tam giác ABC đều có R Δ A B C = 2 a 3 3 ⇒ A B = 2 a .
Dựng hình lăng trụ ABCD.A’B’C’D’, O là trung điểm của B’D’
khi đó B C ' / / A D ' ⇒ B ' A D ' ^ = 60 ∘ ⇒ Δ A B ' D đều cạnh
B ' D ' = 2 a 3 ⇒ A D = 2 a 3 ⇒ A A ' = A ' D 2 − A D 2 = 2 a 2
Lại có:
d A B ' ; B C ' = d B C ' ; A B ' D ' = d B ; A B ' D ' = d A ' ; A ' B ' D ' = A ' H = A ' O . AA' A ' O 2 + A A ' 2 = 2 a 2 3 .
cho hình chóp S.ABC, SA vuông góc (ABC) đáy là tam giác ABC đều cạnh a và SA \(=a\sqrt{3}\)
a) tính góc giữa đường thẳng SB và AB
b) tính góc giữa đường thẳng SC và AC
c) M là trung điểm BC. Tính góc giữa đường thẳng SM và AM
a: \(\widehat{SB;AB}=\widehat{SBA}\)
SA\(\perp\)(ABC)
=>\(SA\perp AB;SA\perp AC;SA\perp BC\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
=>\(\widehat{SBA}=60^0\)
=>\(\widehat{SB;AB}=60^0\)
b:
\(\widehat{SC;AC}=\widehat{SCA}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;AC}=60^0\)
c: ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
Ta có: SA\(\perp\)(ABC)
AM\(\subset\)(ABC)
Do đó: SA\(\perp\)AM
=>ΔSAM vuông tại A
\(\widehat{SM;AM}=\widehat{SMA}\)
Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)
=>\(\widehat{SMA}\simeq63^026'\)
=>\(\widehat{SM;AM}\simeq63^026'\)
a.
Góc giữa SB và AB là góc \(\widehat{SBA}\)
Trong tam giác vuông SAB:
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SBA}=60^0\)
b.
Góc giữa SC và AC là góc \(\widehat{SCA}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
c.
Góc giữa SM và AM là góc \(\widehat{SMA}\)
AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a và S A ⊥ ( A B C ) . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 o Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
![]()
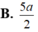
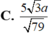
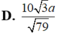
Cho hình chóp S.ABC có đáy ABC là tam giác vuông B , A B = 3 a , B C = 4 a và S A ⊥ A B C . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 ° . Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
A. 5 3 a
B. 5 a 2
C. 5 3 a 79
D. 10 3 a 79
Đáp án D
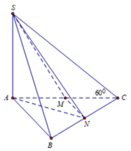
Gọi N là trung điểm của BC
Ta có A B / / M N ⇒ d A B ; S M = d A ; S M N
S A = A C tan 60 ° = 5 a 3
S M = 5 a 3 2 + 5 a 2 2 = 5 a 13 2
S N 2 = S B 2 + B N 2 = S A 2 + A B 2 + B C 2 2 = 5 a 3 2 + 3 a 2 + 2 a 2 = 88 a 2
⇒ S N = 2 a 22
M N = A B 2 = 3 a 2
Ta có:
S M 2 = N S 2 + N M 2 − 2 N S . N M . c o s M N S ^ ⇔ 5 a 13 2 22 = 88 a 2 + 3 a 2 2 − 2.2 a . 22 . 3 a 2 c o s M N S ^
c o s M N S ^ = 3 2 22 ⇒ sin M N S ^ = 79 88
S S M N = 1 2 N M . N S . s i n M N S ⏜ = 1 2 . 3 a 2 .2 a 22 . 79 88 = 3 a 2 79 4
S A M N = 1 4 S A B C = 1 4 . 1 2 .3 a .4 a = 3 a 2 2 ; V S . A M N = 1 3 S A . S A M N = 1 3 .5 a 3 . 3 a 2 2 = 5 a 3 3 2
d A ; S M N = 3 V S . A M N S S M N = 3. 5 a 3 3 2 3 a 2 79 4 = 10 a 3 79
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = 3 a , B C = 4 a và S A ⊥ A B C . Góc giữa đường thẳng SC và mặt phẳng A B C bằng 60 ° . Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
A. 10 3 a 79
B. 5 a 2
C. 5 3 a
D. 5 3 a 79
Đáp án A

Do S A ⊥ A B C nên góc giữ SC và A B C là góc S C A ^ = 60 °
Vì Δ A B C vuông tại B nên A C = 5 a ⇒ S A = 5 a 3
Gọi N là trung điểm BC nên M N / / A B ⇒ A B / / S M N
d A B , S M = d A B , S M N = d A , S M N .
Từ A kẻ đường thẳng song song vơi BC cắt MN tại D.
Do B C ⊥ A B ⇒ B C ⊥ M N ⇒ A D ⊥ M N .
Từ A kẻ AH vuông góc vơi SD
Ta có M D ⊥ A D M D ⊥ S A ⇒ M D ⊥ S A D ⇒ M D ⊥ A H
Mà A H ⊥ S D ⇒ A H ⊥ S M D hay A H ⊥ s m n ⇒ d A , S M N = A H
Do A D = B N = 1 2 B C = 2 a .
Xét Δ S A D có 1 A H 2 = 1 S A 2 + 1 A D 2 = 1 75 a 2 + 1 4 a 2 = 79 300 a 2
⇒ d A B , S M = A H = 10 237 a 79 = 10 3 a 79
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a và S A ⊥ ( A B C ) . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 0 . Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng AB và SM bằng