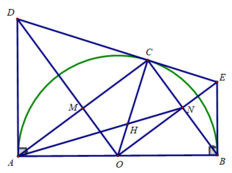
trên nửa đường tròn (O;R) , đường kính AD lấy điểm B và C sao cho ba cung AB, BC, CD bằng nhau. qua C vẽ đường thẳng vuông góc với AD tại H; kéo dài AB cắt tia HC tại T; BD và CH cắt nhau taij E
a. cm HDTB nội tiếp đường tròn
b. gọi F là trung điểm của TE, cm FB là tiếp tuyến của (O)
c. tính diện tich tam giác TAH theo R