Cho cosa = 3/4 vào 270°<a<370° . Tính
A sina , tana , cota
B sin2a , cos2a , tan2a
B sin( a+ π\3 )
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
cho góc nhọn a. chứng minh rằng (cosa-sina)2 - (cosa + sina)2 phần cosa.sina = -4
\(\dfrac{\left(cosa-sina\right)^2-\left(cosa+sina\right)^2}{cosa\cdot sina}\)
\(=\dfrac{\left(cosa-sina-cosa-sina\right)\left(cosa-sina+cosa+sina\right)}{cosa\cdot sina}\)
\(=\dfrac{-2\cdot sina\cdot2\cdot cosa}{cosa\cdot sina}=-4\)
cho cosa =3/4.Tinh A= cos(3a/2)cos(a/2)
cos(\(\dfrac{3a}{2}\))*cos(\(\dfrac{a}{2}\))=\(\dfrac{1}{2}\left(cos\left(\dfrac{3a}{2}+\dfrac{a}{2}\right)+cos\left(\dfrac{3a}{2}-\dfrac{a}{2}\right)\right)\)=\(\dfrac{1}{2}\left(cos\left(2a\right)+cos\left(a\right)\right)\)=\(\dfrac{1}{2}\left(2cos^2a-1+cosa\right)\)=\(\dfrac{1}{2}\left(2\cdot\left(\dfrac{3}{4}\right)^2-1+\dfrac{3}{4}\right)=\dfrac{7}{16}\)
Biết Cosa=3/4 tính sina cota tana
Tan a=12/35 tính sina cota cosa
tana = 3/4.
=>cota=1/ tana =1:3/4=4/3
sina /cosa =tana
=> sina =tana .cosa =3/4. cosa
lại có sin^2(a)+cos^2(a)=1
<=>9/16cos^2(a)+cos^2=1
<=>25/16cos^2(a)=1
<=>cos^2(a)=16/25
=>[cosa =4/5=>sina =3/5
[cosa =-4/5=> sina =-2/5
Cho tana=\(\dfrac{1}{3}\)Tính\(\dfrac{cosa-sina}{cosa+sina}\)
Chứng minh rằng:\(\dfrac{1-tana}{1+tana}=\dfrac{cosa-sina}{cosa+sina}\)
Chứng minh hệ thức sau:
( sina + cosa)2 - ( sina - cosa)2/ sina . cosa = 4
Các bạn giúp mình với!!! Ai nhanh và đúng nhất mình sẽ tick cho!!! Mình cảm ơn!!!!
\(=\frac{\left(\sin a+\cos a-\sin a+\cos a\right)\left(\sin a+\cos a+\sin a-\cos a\right)}{\sin a.\cos a}=\frac{2.\cos a.2.\sin a}{\sin a.\cos a}=4\)
cho sina+cosa=5/4
a, A=sina.cosa b, B= sina-cosa c,C=sin^3a-cos^3a
help me
\(sina+cosa=\frac{5}{4}\Rightarrow\left(sina+cosa\right)^2=\frac{25}{16}\)
\(\Rightarrow sin^2a+cos^2a+2sina.cosa=\frac{25}{16}\)
\(sina.cosa=\frac{\frac{25}{16}-1}{2}=\frac{9}{32}\)
b/ \(\left(sina-cosa\right)^2=sin^2a+cos^2a-2sinacosa\)
\(\left(sina-cosa\right)^2=1-2.\frac{9}{32}=\frac{7}{16}\)
\(\Rightarrow sina-cosa=\pm\frac{\sqrt{7}}{4}\)
c/ \(sin^3a-cos^3a=\left(sina-cosa\right)\left(sin^2a+cos^2a+sina.cosa\right)\)
\(=\left(sina-cosa\right)\left(1+\frac{9}{32}\right)=\pm\frac{41\sqrt{7}}{128}\)
Cho góc α thỏa mãn cos a = 3 5 v à - π 2 < a < 0 .Tính 5 + 3 tan α + 6 - 4 c o t α
A. 4
B. -2
C. -6
D. 3
Chọn A.
Ta có 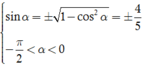
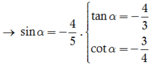
Thay 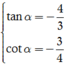 vào P ta được P = 4.
vào P ta được P = 4.
cho a nhọn biet sina-cosa=3/5 tinh gia tri cua bieu thuc e=sina*cosa bang