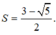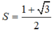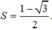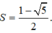a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).