a) Ta có:  \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1;{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2};\overrightarrow i .\overrightarrow j  = 0\)(vì \(\overrightarrow i  \bot \overrightarrow j \) )

b) Ta có: \(\overrightarrow u .\overrightarrow v  = \left( {{x_1}\overrightarrow i  + {y_1}\overrightarrow j } \right).\left( {{x_2}\overrightarrow i  + {y_2}\overrightarrow j } \right) = {x_1}{x_2}.{\overrightarrow i ^2} + {x_1}{y_2}.\left( {\overrightarrow i .\overrightarrow j } \right) + {y_1}{x_2}.\left( {\overrightarrow j .\overrightarrow i } \right) + {y_1}{y_2}.{\overrightarrow j ^2} = {x_1}{x_2} + {y_1}{y_2}\)

\(\overrightarrow{a}=\left(2;-1\right)\)

C. cả 2 cái trên

Giả sử `\vec{c}=m\vec{a}+n\vec{b}`

`<=>(3;-4)=m(2;0)+n(0;-3)`

`<=>(3;-4)=(2m;-3n)`

`<=>{(m=3/2),(n=4/3):}`

   `=>\vec{c}=3/2\vec{a}+4/3\vec{b}`

hongg bt lm 

Đáp án D

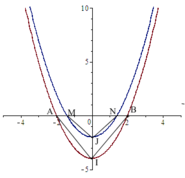
Phép tịnh tiến theo v → 0 ; b  biến parabol P : y = x 2 − 4  thành parabol  P ' : y = x 2 − 4 + b

Giao điểm của A,B với Ox của (P) có tọa độ lần lượt là:  − 2 ; 0 , 2 ; 0

Giao điểm M,N với Ox của (P) có toạn độ lần lượt là:  − 4 − b ; 0 , 4 − b ; 0

Đỉnh I,J của parabon (P), (P') có tọa độ lần lượt:  0 ; − 4 , 0 ; − 4 + b

Diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN nên ta có:

I O . A B = 8 J O . M N ⇔ 4.4 = 8. 4 − b .2 4 − b ⇔ 4 − b 3 = 1 ⇔ b = 3 ⇒ J 0 ; − 1

Ta có  a → = m . u → + v → = 4 m + 1 ; m + 4 b → = i → + j → = 1 ; 1 .

Yêu cầu bài toán  ⇔ cos a → , b → = cos 45 0 = 2 2

⇔ 4 m + 1 .1 + m + 4 .1 2 4 m + 1 2 + m + 4 2 = 2 2 ⇔ 5 m + 1 2 17 m 2 + 16 m + 17 = 2 2

⇔ 5 m + 1 = 17 m 2 + 16 m + 17 ⇔ m + 1 ≥ 0 25 m 2 + 50 m + 25 = 17 m 2 + 16 m + 17 ⇔ m = − 1 4 .

Chọn C.

Chọn B