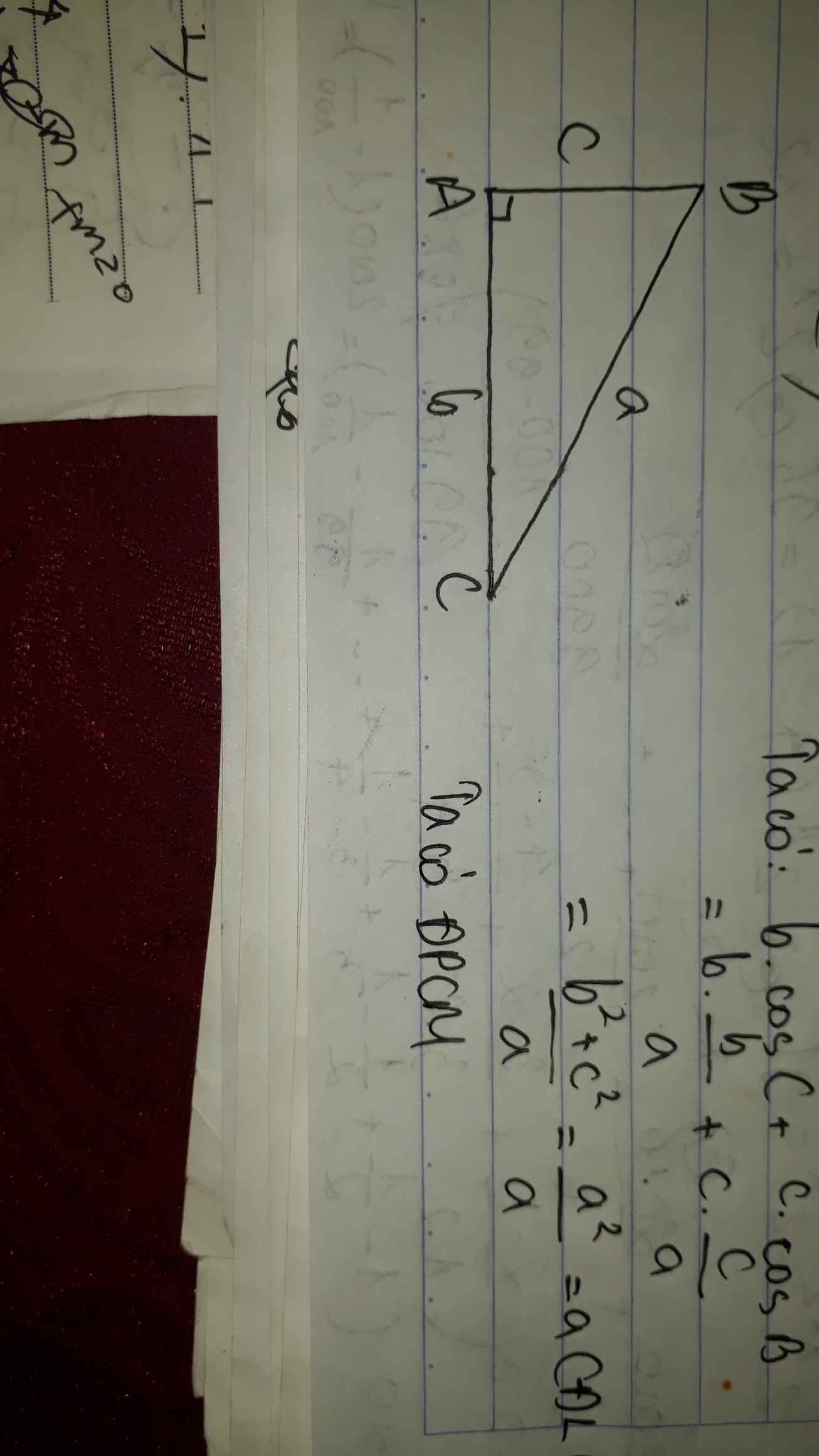chứng minh rằng tam giác ABC vuông nếu: cosB + cosC = \(\frac{b+c}{a}\)
NM
Những câu hỏi liên quan
Chứng minh rằng trong mọi tam giác ABC ta đều có:
a, a = b cosC + c cosB;
b, sinA = sinBcosC + sinCcosB;
c, ha = 2RsinBsinC.
a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
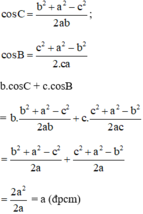
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
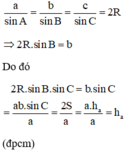
Đúng 0
Bình luận (0)
Cho tam giác ABC chứng minh rằng
Nếu b/cosB + c/cosC = a/sinb.sinC thì ABC vuông tại A
Cho tam giác ABC có ba cạnh a,b,c. Chứng minh rằng:
\(\dfrac{a^2+b^2+c^2}{2abc}=\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(=\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}\)
\(=\dfrac{a^2+b^2+c^2}{2abc}\) (đpcm)
Đúng 1
Bình luận (0)
a2 = b2 + c2 - 2bc.cosA
b2 = a2 + c2 - 2ac.cosB
c2 = a2 + b2 - 2ab.cosC
⇒ a2 + b2 + c2 = 2bc.cosA + 2ac.cosB + 2ab.cosC
⇒ VT = \(\dfrac{2bc.cosA}{2abc}+\dfrac{2ab.cosC}{2abc}+\dfrac{2ac.cosB}{2abc}\)
⇒ VT = \(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, BC = a, CA = b, AB = c. Chứng minh rẳng:
a = b. cosC + c. cosB.
Áp dụng hệ quả của định lý Cosin ta có:
\(\cos C=\dfrac{b^2+a^2-c^2}{2ab};\cos B=\dfrac{c^2+a^2-b^2}{2ca}\)
\(\Rightarrow b\cos C+c\cos B=b\dfrac{b^2+a^2-c^2}{2ab}+c\dfrac{c^2+a^2-b^2}{2ca}=\)
\(\dfrac{b^2+a^2-c^2}{2a}+\dfrac{c^2+a^2-b^2}{2a}=\dfrac{2a^2}{2a}=a\)
Đúng 0
Bình luận (0)
cho tam giác ABC chứng minh rằng:
cosA+cosB-cosC= \(4cos\frac{A}{2}.cos\frac{B}{2}.sin\frac{C}{2}-1\)
\(cosA+cosB-cosC=2cos\frac{A+B}{2}.cos\frac{A-B}{2}+2sin^2\frac{C}{2}-1\)
\(=2sin\frac{C}{2}.cos\frac{A-B}{2}+2sin^2\frac{C}{2}-1\)
\(=2sin\frac{C}{2}\left(cos\frac{A-B}{2}+sin\frac{C}{2}\right)-1\)
\(=2sin\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)-1\)
\(=4cos\frac{A}{2}cos\frac{B}{2}sin\frac{C}{2}-1\)
Đúng 0
Bình luận (0)
cho tam giác ABC bất kì . chứng minh rằng \(1+\frac{1}{2}x^2\ge cosA+x\left(cosB+cosC\right)\) với mọi x thuộc R ( A;B;C là số đo 3 góc của 1 tam giác)
Ta có bất phương trình tương đương:
\(\Leftrightarrow x-2\left(\cos B+\cos C\right)x+2-2\cos A\ge0\)
Ta có:
\(\Delta'=\left(\cos B+\cos C\right)^2-2+2\cos A\)
\(=4\cos^2\left(\frac{B+C}{2}\right).\cos^2\left(\frac{B-C}{2}\right)-4\sin^2\left(\frac{A}{2}\right)\)
\(=4\sin^2\left(\frac{A}{2}\right)\left(\cos^2\left(\frac{B-C}{2}\right)-1\right)\le0\)
Bên cạnh đó ta có hệ số \(a=1>0\)
Từ đây ta suy ra điều phải chứng minh là đúng.
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, BC = a, CA = b, AB = c. Chứng minh rẳng:
a = b. cosC + c. cosB.
Cho tam giác ABC nhọn. Chứng minh rằng cosA + cosB + cosC = AB^2 + AC^2 + BC^2/4.S.ABC
Xét tam giác ABC nhọn có \(BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos\widehat{A}\)
\(\Rightarrow\cos\widehat{A}=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4\cdot\dfrac{1}{2}AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4S_{ABC}}\)
Cmtt: \(\left\{{}\begin{matrix}\cos\widehat{B}=\dfrac{AB^2+BC^2-AC^2}{4S_{ABC}}\\\cos\widehat{C}=\dfrac{AC^2+BC^2-AB^2}{4S_{ABC}}\end{matrix}\right.\)
\(\Rightarrow\cos\widehat{A}+\cos\widehat{B}+\cos\widehat{C}\\
=\dfrac{AB^2+AC^2-BC^2+AB^2+BC^2-AC^2+AC^2+BC^2-AB^2}{4S_{ABC}}\\
=\dfrac{AB^2+AC^2+BC62}{4S_{ABC}}\)
Đúng 0
Bình luận (0)
chứng minh rằng nếu tam giác ABC thỏa mãn điều kiện \(\dfrac{sinA}{sinB}=\dfrac{cosB+cosC}{cosC+cosA}\)thì tam giác ABC vuông hoặc cân