a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
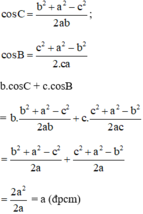
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
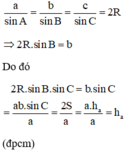
a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
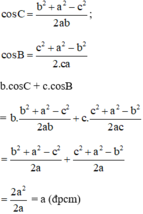
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
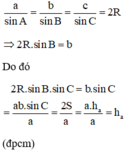
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:
1, sin A + sin B - sin C = 4sin\(\dfrac{A}{2}\) sin \(\dfrac{B}{2}\)sin \(\dfrac{C}{2}\)
2, \(\dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}=tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\) (ΔABC nhọn)
3, \(\dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}=tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\)
GIÚP MÌNH VỚI!!!
Trong hệ trục 0xy, cho A(1;1); B(2;4); C(10;-2)
a)Chứng minh tam giác ABC vuông
b)Tính \(\overrightarrow{BA}\).\(\overrightarrow{BC}\); cosB; cosC
Tìm tính chất của tam giác ABC thỏa:
sinA+sinB+sinC=1-cosA+cosB+cosC
Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
A. CosB + Cos C = 2 Cos A B. Sin B + Sin C = 2 Sin A
C. Sin B + Sin C = \(\dfrac{1}{2}SinA\) D. Sin B + Sin C = 2 Sin A
Chứng minh rằng với mọi tam giác ABC, ta có a = 2RsinA, b = 2RsinB, c = 2RsinC, trong đó R là bán kính đường tròn ngoại tiếp tam giác.
Chứng minh công thức hình chiếu
a, a= b cosC + c cosB
b, a= r(cotB/2+cotC/2)
Cho cosa=sinB/sinA, cosb=sinC/sinA, cos(a+b)=sinBsinC, chứng minh tan2A=tan2B+tan2C
Cho tam giác ABC có góc A tù. Cho các biểu thức sau:
(1) M = sin A + sin B + sin C
(2) N = cosA. cosB. cosC
(3) P = cos A 2 . sin B 2 . c o t C 2
(4) Q = cotA.tan B.tan C
Số các biểu thức mang giá trị dương là:
A. 1
B. 2
C. 3
D. 4
Hãy chứng minh công thức sin(a + b) = sina cosb + cosa sinb.