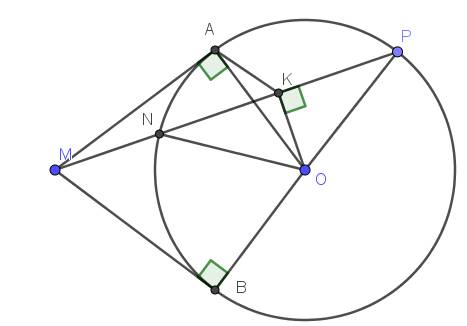
Từ 1 điểm A ở ngoài (O;R) kẻ 2 tiếp tuyến AB,AC với (O) (B,C là 2 tiếp điểm )
a)C/m 4 điểm A,B,O,C cùng thuộc 1 đường tròn
b)Đường thẳng qua B và song song với OC cắt đường thẳng qua C và song song với OB tại F . C/m tg BFCO là h.thoi và A,F,O thẳng hàg
c)X.định vị trí của A sao cho SABC = 2SBFCO
d)Trong tam giác ABC , c/m sin2B - cos2B =cosA