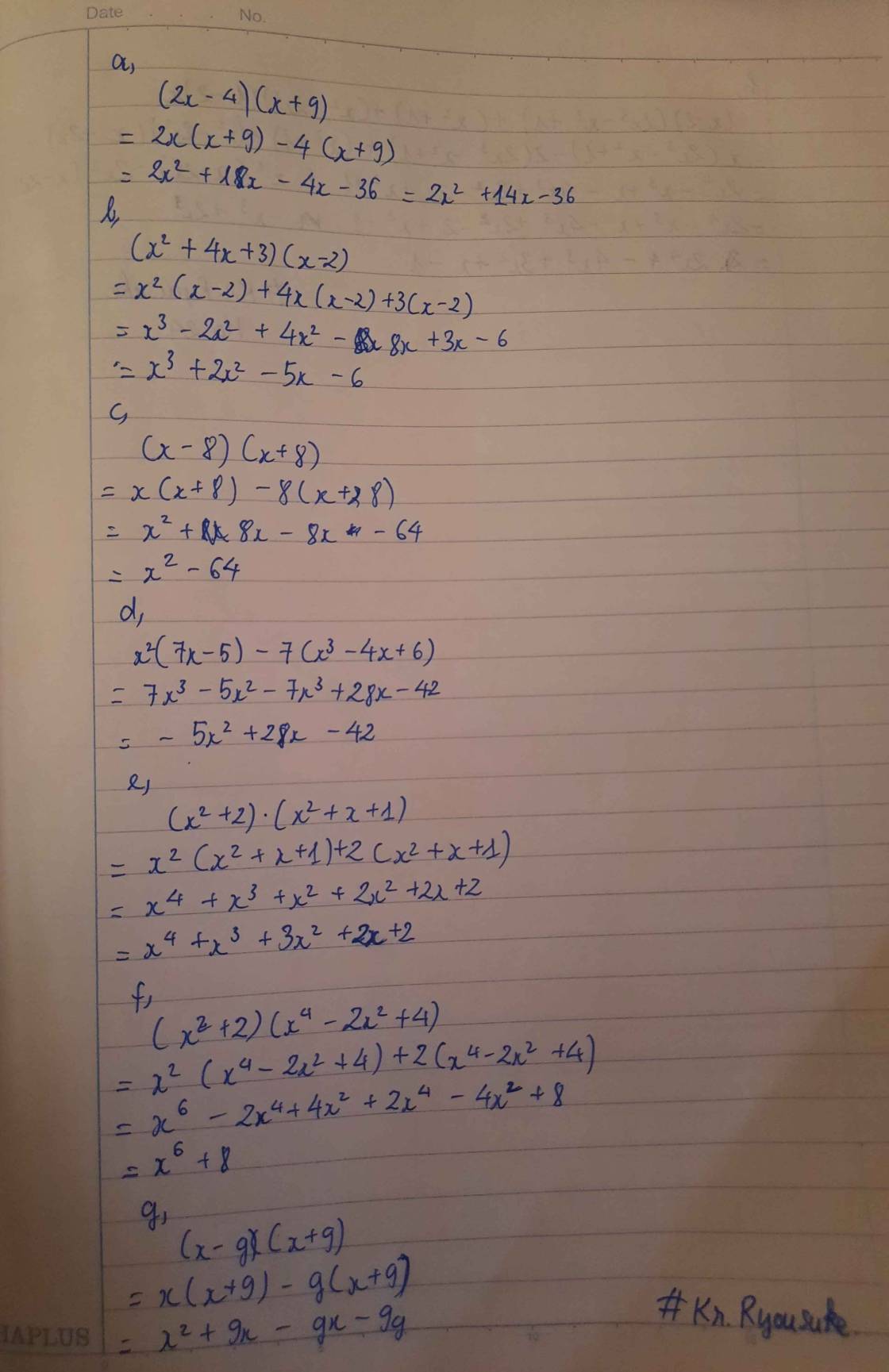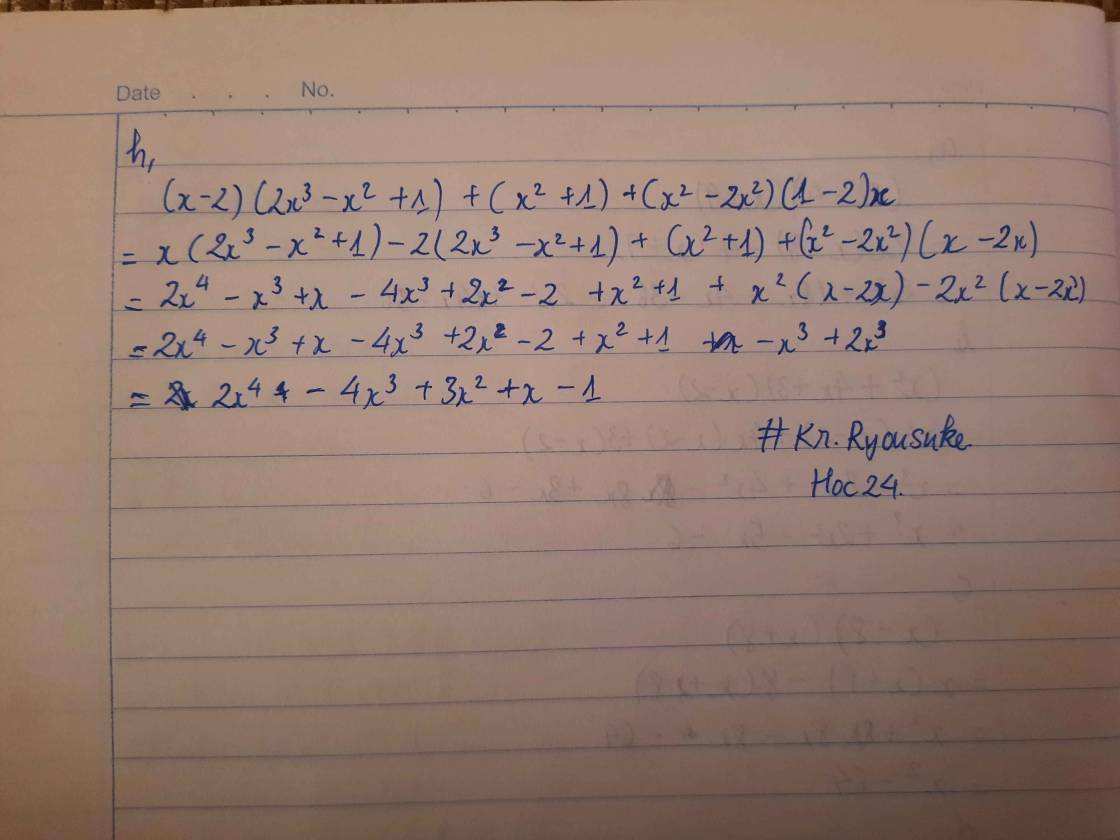(x+8)(x+6)-x2=104
DT
Những câu hỏi liên quan
Tìm x,biết:
a) (x+8)(x+6)-x2 =104
* ĐỀ như dưới phải ko ??? Ai lại ghi x2 bao giờ ??
a) (x + 8)(x + 6) - x2 =104
\(\Leftrightarrow\) x2 + 6x + 8x + 48 - x2 = 104
\(\Leftrightarrow\) 14x + 48 = 104
\(\Leftrightarrow\) 14x = 56
\(\Leftrightarrow\) x = 4
Đúng 1
Bình luận (0)
Tính giá trị của biểu thức:
a) x2 – y2 tại x = 87 và y = 13
b) x(x2 + xy + y2) – y(x2 + xy + y2) tại x = 10 và y = -1
c) x3 + 6x2 + 12x + 8 tại x = 8
d) x2 – 8x + 17 tại x = 104
a: \(=\left(x-y\right)\left(x+y\right)\)
\(=74\cdot100=7400\)
c: \(=\left(x+2\right)^3\)
\(=10^3=1000\)
Đúng 0
Bình luận (0)
a) \(=\left(x-y\right)\left(x+y\right)\)
Thay \(x=87;y=13\) ta đc: \(\left(87-13\right)\left(87+13\right)=74\cdot100=7400\)
b)\(=\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-y^3\)
Thay \(x=10;y=-1\) ta đc:
\(10^3-\left(-1\right)^3=1000-1=999\)
c)\(=\left(x+2\right)^3\)
Thay \(x=8\) ta đc: \(\left(8+2\right)^3=10^3=1000\)
d)\(=x^2-8x+16+1=\left(x-4\right)^2+1\)
Thay \(x=104\) ta đc: \(\left(104-4\right)^2+1=100^2+1=10001\)
Đúng 1
Bình luận (0)
(x+8)(x+6)-x^2 =104
Ta có:
(x+8)(x+6)-x^2=104
x^2+6x+8x+48-x^2=104
14x+48=104
14x=104-48
14x=56
x=4
Đúng 0
Bình luận (0)
(x+8)(x+6)-x2=104
<=> x2+6x+8x+48-x2=104
<=> 14x+48=104
<=> 14x=104-48
<=> 14x=56
<=> x= 56:14
<=> x=4
Đúng 0
Bình luận (0)
x +110/100 + x+8/102 + x+6/104 =x+4/106 x+2/108
\(\frac{x+110}{100}+\frac{x+8}{102}+\frac{x+6}{104}=\frac{x+4}{106}+\frac{x+2}{108}\)
\(\Leftrightarrow\frac{x+110}{100}+\left(\frac{x+8}{102}+1\right)+\left(\frac{x+6}{104}+1\right)=\left(\frac{x+4}{106}+1\right)+\left(\frac{x+2}{108}+1\right)\)
\(\Leftrightarrow\frac{x+110}{100}+\frac{x+110}{102}+\frac{x+110}{104}=\frac{x+110}{106}+\frac{x+110}{108}\)
\(\Leftrightarrow\frac{x+110}{100}+\frac{x+110}{102}+\frac{x+110}{104}-\frac{x+110}{106}-\frac{x+110}{108}=0\)
\(\Leftrightarrow\left(x+110\right)\left(\frac{1}{100}+\frac{1}{102}+\frac{1}{104}+\frac{1}{106}+\frac{1}{108}\right)=0\)
\(\Leftrightarrow x+110=0\) (vì \(\frac{1}{100}+\frac{1}{102}+\frac{1}{104}-\frac{1}{106}-\frac{1}{108}>0\))
\(\Leftrightarrow x=-110\)
Vậy \(x=-110\)
Đúng 0
Bình luận (0)
x +110/100 + x+8/102 + x+6/104 =x+4/106 x+2/108
Thực hiện phép tính:
a,(2x- 4)(x+9)
b,(x2 + 4x +3)(x-2)
c,(x-8)(x+8)
d, x2(7x-5)-7(x3- 4x+6)
e,(x2+2)(x2+x+1)
f,(x2+2)(x4-2x2+4)
g,(x-g)(x+9)
h,(x-2)(2x3-x2+1)+(x2+1)+(x2-2x2)(1-2)x
Dễ
Thế
Mà
Cũnhoir
Dc
Ạ
Chịu
Chắc
Phải
Ngu
Lamqs
Mới
Hỏi
Câu
Này
Đúng 1
Bình luận (0)
Tính số phần tử của các tập hợp sau :
a) A là tập hợp các số tự nhiên X mà X + 6 = 8
b) B = { 2; 4; 6; 8; ...; 102; 104 }
a) Ta có:
\(X+6=8\)
\(\Rightarrow X=8-6\)
\(\Rightarrow X=2\)
Vậy: \(A=\left\{2\right\}\)
Có 1 phần tử
b) Số phần tử của tập hợp B là:
\(\left(104-2\right):2+1=52\) (số hạng)
Đúng 3
Bình luận (0)
tìm x
x+5/7=7/8:1/6
15/6-x=5/8×2/15
rút gọn
72/104
điền số tự nhiên thích hợp vào chỗ có dấu chấm
3/13<..../13<......../13<......../13<....../13<......./13<72/104
\(x+\frac{5}{7}=\frac{7}{8}:\frac{1}{6}\)
\(\Leftrightarrow x+\frac{5}{7}=\frac{21}{4}\)
\(\Leftrightarrow x=\frac{127}{28}\)
\(\frac{72}{104}=\frac{72:8}{104:8}=\frac{9}{13}\)
\(\frac{3}{13}< \frac{4}{13}< \frac{5}{13}< \frac{6}{13}< \frac{7}{13}< \frac{8}{13}< \frac{72}{104}=\frac{9}{13}\)
Đúng 0
Bình luận (0)
Tìm x :
a ) \(x+\frac{5}{7}=\frac{7}{8}\div\frac{1}{6}=\frac{7\times6}{8\times1}=\frac{21}{4}\)
\(x=\frac{21}{4}-\frac{5}{7}=\frac{127}{28}\)
b ) \(\frac{15}{6}-x=\frac{5}{8}\times\frac{2}{15}=\frac{1}{12}\)
\(x=\frac{15}{6}-\frac{1}{12}=\frac{29}{12}\)
Rút gọn : \(\frac{72}{104}=\frac{72\div8}{104\div8}=\frac{9}{13}\)
Điền STN thích hợp :
\(\frac{3}{13}< \frac{4}{13}< \frac{5}{13}< \frac{6}{13}< \frac{7}{13}< \frac{8}{13}< \frac{9}{13}\left(\frac{72}{104}\right)\)Những số cần điền là : 4, 5, 6, 7, 8 .
==========> CHÚC HỌC GIỎI NHỚ K MÌNH <==========
Đúng 0
Bình luận (0)
Bài 2: Tìm x, biết:
a) 4x(x + 1) = 8( x + 1) c) x2 – 6x + 8 = 0
b) x3 + x2 + x + 1 = 0 d) x3 – 7x – 6 = 0
\(a,\Leftrightarrow\left(4x-8\right)\left(x+1\right)=0\\ \Leftrightarrow4\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ b,\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=-1\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow x=-1\\ c,\Leftrightarrow x^2-2x-4x+8=0\\ \Leftrightarrow\left(x-2\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\\ d,\Leftrightarrow x^3-3x^2+3x-9x+2x-6=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+x+2x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a) \(\Rightarrow4\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
b) \(\Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x^2+1\right)=0\)
\(\Rightarrow x=-1\left(do.x^2+1\ge1>0\right)\)
c) \(\Rightarrow x\left(x-4\right)-2\left(x-4\right)=0\)
\(\Rightarrow\left(x-4\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
d) \(\Rightarrow x^2\left(x-3\right)+3x\left(x-3\right)+2\left(x-3\right)\)
\(\Rightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)
\(\Rightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\\x=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)