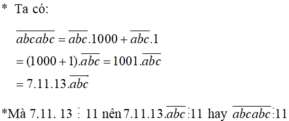chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn: 328328 chia hết cho 11)
HT
Những câu hỏi liên quan
Chứng tỏ rằng số có dạng (abcabc) bao giờ cũng chia hết cho 11 ( chẳng hạn 328328 ⋮11)
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn: 328328 chia hết cho 11)
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn 328328 chia hết cho 11)
Theo bài ra ta có :
\(\overline{abcabc}\)
\(=\overline{abc}.1000+\overline{abc}.1\)
\(=\overline{abc}.\left(1000+1\right)\)
\(=\overline{abc}.1001\)
\(=\overline{abc}.11.91\)
\(=\left(\overline{abc}.91\right).11\)
\(\Rightarrow\overline{abcabc}⋮11\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Ta có:
\(\overline{abcabc}=1001\overline{abc}=11.91\overline{abc}\)
Vì \(11.91\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11
\(\Rightarrow\) ĐPCM(điều phải chứng minh)
Đúng 0
Bình luận (0)
abcabc \(⋮\) 11 vì:
abcabc = abc . 1000 + abc
abcabc = abc . ( 1000 + 1 )
abcabc = abc . 1001
abcabc = abc . 11 . 91
Mà 11 \(⋮\) 11 \(\Rightarrow\) abc . 11 . 91 \(⋮\) 11
Vậy abcabc \(⋮\) 11 ( đpcm )
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 ( chẳng hạn số 328328 chia hết cho 11 )
Ta có:
\(\overline{abcabc}=1001\overline{abc}=11.99\overline{abc}\)
Vì \(11.99\overline{abc}\) \(⋮\) 11 nên \(\overline{abcabc}\) \(⋮\) 11
\(\Rightarrow\text{Điều phải chứng minh}\)
Đúng 0
Bình luận (0)
Vì x ⋮ 11 <=> (a0+a2+a4+...) - (a1+a3+a5+...) ⋮ 11
=> (c+a+b) - (b+c+a) = 0 ⋮ 11
Vậy dạng abcabc bao giờ cũng chia hết cho 11.
Đúng 0
Bình luận (0)
abcabc=a.100000+b.10000+c.1000+a.100+b.10+c.1
=a.100100+b.10010+c.1001
=a00.1001+b0.1001+c.1001
=abc.1001
=(abc.91).11 chia hết cho 11
=> abcabc chia hết cho 11
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 (chẳng hạn 328328 chia hết cho 11)
Có abcabc = abc . 1000 + abc
abcabc = abc . ( 1000 + 1 )
abcabc = abc . 1001
abcabc = abc . 11 . 91
Mà 11 \(⋮\)11 nên abc . 11 . 91 \(⋮\) 11
Vậy abcabc \(⋮\) 11 ( đpcm )
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11( chẳng hạn 328328 chia hết cho 11 )
Chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11(chẳng hạn 328328 chia hết cho 11)
\(\overline{abcabc}=\overline{abc}.1001=\overline{abc}.91.11\)
\(\Rightarrow\overline{abcabc}⋮11\)
Vậy số có dạng \(\overline{abcabc}\)bao giờ cũng chia hết cho 11
Đúng 0
Bình luận (0)
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 ( chẳng hạn : 328328 chia hết cho 11 )
abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11
chứng tỏ rằng số có dạng abcabc bao giờ cũng chia hết cho 11 ( chẳng hạn : 328328 chia hết cho 11 ) - Tìm với Google
Đúng 0
Bình luận (0)
Ta có:
abcabc=abc*1001
Mà 1001 chia hết cho 11 và abcEN
=>abc*1001 chia hết cho 11
Vậy........
Đúng 0
Bình luận (0)
Chứng tỏ rằng số có dạng \(\overline{abcabc}\) bao giờ cũng chia hết cho 11 (chẳng hạn \(328328⋮11\)) ?
Ta có : \(\overline{abcabc}=\overline{abc}.1001=\overline{abc}.11.91⋮11\)
\(\Rightarrow\overline{abcabc}⋮11\)
Đúng 0
Bình luận (0)
Ta có \(\overline{abcabc}=\overline{abc}.1001\)
\(=\overline{abc}.11.91⋮11\)
\(=>\overline{abcabc}⋮11\left(dpcm\right)\)
Đúng 0
Bình luận (0)