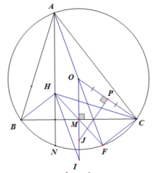
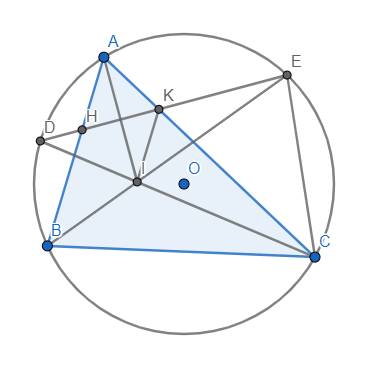
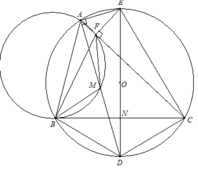
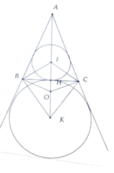
Cho tam giác cân ABC ( AB = AC) nội tiếp đường tròn (O). Gọi D là trung điểm của AC; tiếp tuyến của đường tròn (O) tại A cắt tia BD tại E. Tia CE cắt (O) tại F.
1.Chứng minh BC // AE.
2.Chứng minh ABCE là hình bình hành.
3.Gọi I là trung điểm của CF và G là giao điểm của BC và OI. So sánh góc BAC và BGO.