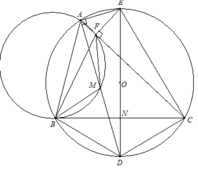
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB<AC. Đường phân giác của góc B A C ^ cắt (O) tại điểm D khác A
Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O.
Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA
1) Chứng minh rằng tam giác ĐM và tam giác BCF đồng dạng.
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O).
D là điểm thuộc cạnh BC (D khác B và D khác C).
Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F.
Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M.
Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N.
2) Giả sử F N E M = B N C M . Chứng minh rằng AD là phân giác của tam giác ABC.
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). D là điểm thuộc cạnh BC (D khác B và D khác C).
Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F.
Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M.
Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N.
1) Chứng minh rằng đường thẳng MN tiếp xúc với (O).
Cho tam giác ABC nhọn với AB<BC và D là điểm thuộc cạnh BC sao cho AD là phân giác của B A C ^ .
Đường thẳng qua C và song song với AD, cắt trung trực của AC tại E.
Đường thẳng qua B song song với AD, cắt trung trực của AB tại F.
1) Chứng minh rằng tam giác ABF đồng dạng với tam giác ACE.
2). Chứng minh rằng các đường thẳng B E ; C F ; A D đồng quy tại một điểm, gọi điểm đó là G.
3). Đường thẳng qua G song song với AE cắt đường thẳng BF tại Q. Đường thẳng QE, cắt đường tròn ngoại tiếp tam giác GEC tại P khác E. Chứng minh rằng các điểm A, P, G, Q, F cùng thuộc một đường tròn.
Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
2). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác △ C E F .
3). Gọi giao điểm của OC và BD là I, chứng minh rằng I B . B E . E I = I D . D F . F I .
Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
2). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác △ C E F .
3). Gọi giao điểm của OC và BD là I, chứng minh rằng I B . B E . E I = I D . D F . F I .
Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và AB<CD.
M là trung điểm CD. P là điểm di chuyển trên đoạn MD ( P khác M, D ).
AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B, QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E
1) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác AQF luôn thuộc một đường thẳng cố định khi P di chuyển.
