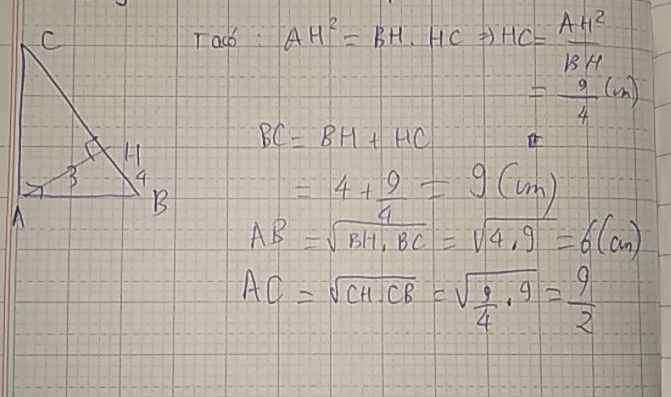Cho ABC vuông tại A có AB = 3cm, AC = 4cm và AH là đường cao. Tính BC,
BH, HC và AH.
MB
Những câu hỏi liên quan
a) Cho tam giác ABC vuông tại A, đường cao AH.
Biết AB = 8cm, BH = 4cm. Tính: BC, HC, AH.
b) Cho tam giác ABC vuông tại A, đường cao AH.
Biết AB = 6cm, BH = 3cm. Tính: BC, HC, AH.
a: \(AH=4\sqrt{3}\left(cm\right)\)
HC=12cm
BC=16cm
Đúng 1
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AB 9cm, BC 15cm. Tính BH, HC b) Biết BH 1cm, HC 3cm. Tính AB, AC c) Biết AB 6cm, AC 8cm. Tính AH, BCBài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, BH 2,4cm a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc BBài 3: Cho tam giác ABC có BC 9cm, góc B 60 độ, góc C 40 độ, đường cao AH. Tính AH, AB, AC
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB= 9cm, BC= 15cm. Tính BH, HC
b) Biết BH= 1cm, HC= 3cm. Tính AB, AC
c) Biết AB= 6cm, AC= 8cm. Tính AH, BC
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB= 3cm, BH= 2,4cm
a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc B
Bài 3: Cho tam giác ABC có BC= 9cm, góc B= 60 độ, góc C= 40 độ, đường cao AH. Tính AH, AB, AC
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH=3cm, BH=4cm. Tính độ dài các đoạn thẳng HC,BC,AB,AC
Ta có:
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=\dfrac{9}{4}\left(cm\right)\)
\(BC=BH+HC=4+\dfrac{9}{4}=9\left(cm\right)\)
\(AB=\sqrt{BH.BC}=\sqrt{4.9}=6\left(cm\right)\)
\(AC=\sqrt{CH.BC}=\sqrt{\dfrac{9}{4}.9}=\dfrac{9}{2}\left(cm\right)\)
Đúng 2
Bình luận (0)
\(AH^2=BH.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích hai hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=2,25cm\)
\(BC=BH+HC=4+2,25=6,25cm\)
\(AB^2=BH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giwac hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow AB=\sqrt{BH.BC}=\sqrt{4.6,25}=5cm\)
\(AC=\sqrt{BC^2-AB^2}\) (Pitago)
\(\Rightarrow AC=\sqrt{6,25^2-5^2}=3,75cm\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH24 cm và HC18 cm.
Tính: BH, ,BC,AC,AB và diện tích tam giác ABC
Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB 12 cm và BC20 cm.
Tính: BH, ,AC,HC,AH và diện tích tam giác ABC
Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB3 cm và AC4 cm.
Tính: BH, ,BC,HC,AH và diện tích tam giác ABC
Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC15 cm và AH 12 cm.
Tính: BH, ,BC,A...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH.
a, biết AB = 3cm, AC = 4cm. Tính BH; AH
b, HB = 2cm, HC = 8cm. Tính AH
c, biết AB/AC =3/4; BC = 10cm. Tính AC
Cho tam giác ABC vuông tại A, đường cao AH
a, Biết AH = 6cm, BH = 4,5cm. Tính AB, AC, BC, HC
b, Biết AB = 6cm, BH = 3cm. Tính AH và tính chu vi của các tam giác vuông trong hình
a, AB = 7,5cm, AC = 10cm, BC = 12,5cm, HC = 8cm
b, AH = 3 3 cm; P A B C = 18 + 6 3 c m ; P A B H = 9 + 3 3 c m ; P A C H = 9 + 9 3 c m
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH a, Biết AH = 6 cm , BH = 4,5 cm . Tính AB , AC , BC, HC b, Biết AB=6 cm , BH = 3cm . Tính AH , AC ,HC
Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AH = 6cm, BH=4,5cm. Tính AB,AC,BC,HC. b) Biết AB = 6cm, BH=3cm. Tính AH,AC,CH
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6 cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6 a) tính độ dài AH, AB, AC b) Gọi M là trung điểm của AC. Tính số đo góc AMB ( làm tròn đến độ)
a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (0)