Giải pt bằng cách đặt 1 ẩn phụ
x2+\(\sqrt{x+1}=1\)
giải PT bằng cách đặt 1 ẩn phụ
\(x-\sqrt{x-1}-3=0\)
ĐKXĐ : \(1\le x\le3\)
\(x-\sqrt{x-1}-3=0\)
\(\Leftrightarrow\left(x-1\right)-\sqrt{x-1}-2=0\)
Đặt \(t=\sqrt{x-1},t\ge0\), suy ra pt trên trở thành \(t^2-t-2=0\Leftrightarrow\left(t-2\right)\left(t+1\right)=0\Leftrightarrow\orbr{\begin{cases}t=2\left(\text{nhận}\right)\\t=-1\left(\text{loại}\right)\end{cases}}\)
Với t = 2 suy ra x = 5
Giải phương trình bằng cách đặt ẩn phụ: 3 . x 2 + x 2 - 2 x 2 + x - 1 = 0
3.(x2 + x)2 – 2(x2 + x) – 1 = 0 (1)
Đặt t = x2 + x,
Khi đó (1) trở thành : 3t2 – 2t – 1 = 0 (2)
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1; t2 = c/a = -1/3.
+ Với t = 1 ⇒ x2 + x = 1 ⇔ x2 + x – 1 = 0 (*)
Có a = 1; b = 1; c = -1 ⇒ Δ = 12 – 4.1.(-1) = 5 > 0
(*) có hai nghiệm
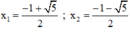
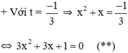
Có a = 3; b = 3; c = 1 ⇒ Δ = 32 – 4.3.1 = -3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 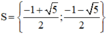
giải pt sau bằng phương pháp đặt ẩn phụ : \(\sqrt{x+1}-\sqrt{x}-\sqrt{x^2+x}=1-x\)
Lời giải:
ĐK: $x\geq 0$
Đặt $\sqrt{x+1}=a; \sqrt{x}=b$. ĐK $a,b\geq 0$ thì ta có:
$a-b-ab=a^2-2b^2$
$\Leftrightarrow a-b=a^2+ab-2b^2=(a-b)(a+2b)$
$\Leftrightarrow (a-b)(a+2b-1)=0$
$\Leftrightarrow a=b$ hoặc $a+2b=1$
Nếu $a=b\Rightarrow a^2=b^2\Leftrightarrow x+1=x$ (vô lý)
Nếu $a+2b=1$
$\Leftrightarrow \sqrt{x+1}-1+2\sqrt{x}=0$
$\Leftrightarrow \frac{x}{\sqrt{x+1}+1}+2\sqrt{x}=0$
$\Leftrightarrow \sqrt{x}(\frac{\sqrt{x}}{\sqrt{x+1}+1}+2)=0$
Dễ thấy biểu thức trong ngoặc lớn hơn $0$ nên \sqrt{x}=0$
$\Leftrightarrow x=0$
Vậy.......
Giải phương trình sau bằng cách đặt ẩn phụ:
\(\dfrac{x}{\sqrt{4x-1}}+\dfrac{\sqrt{4x-1}}{x}=2\)
Đặt \(\dfrac{x}{\sqrt{4x-1}}=a\)
Theo đề, ta có phương trình:
a+1/a=2
\(\Leftrightarrow a+\dfrac{1}{a}=2\)
\(\Leftrightarrow\dfrac{a^2+1-2a}{a}=0\)
=>a=1
=>\(x=\sqrt{4x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=4x-1\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=3\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow x\in\left\{2+\sqrt{3};2-\sqrt{3}\right\}\)
giải hệ pt bằng cách đặt ẩn phụ
\(\dfrac{3}{2x-y}-\dfrac{6}{x+y}=1\)
\(\dfrac{1}{2x-y}-\dfrac{1}{x+y}=0\)
đặt 1/2x-y là a
1/x+y là b
hpt ta đc:
3.a-6.b=1
a-b=0
( giải đi pạn)
Giải phương trình bằng cách đặt ẩn phụ:
a ) 3. x 2 + x 2 − 2 x 2 + x − 1 = 0 b ) x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 c ) x − x = 5 x + 7 d ) x x + 1 − 10 ⋅ x + 1 x = 3
a)
3 · x 2 + x 2 - 2 x 2 + x - 1 = 0 ( 1 )
Đặt t = x 2 + x ,
Khi đó (1) trở thành : 3 t 2 – 2 t – 1 = 0 ( 2 )
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 ; t 2 = c / a = - 1 / 3 .
+ Với t = 1 ⇒ x 2 + x = 1 ⇔ x 2 + x – 1 = 0 ( * )
Có a = 1; b = 1; c = -1 ⇒ Δ = 1 2 – 4 . 1 . ( - 1 ) = 5 > 0
(*) có hai nghiệm
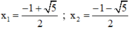
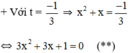
Có a = 3; b = 3; c = 1 ⇒ Δ = 3 2 – 4 . 3 . 1 = - 3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 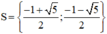
b)
x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 ⇔ x 2 − 4 x + 2 2 + x 2 − 4 x + 2 − 6 = 0 ( 1 )
Đặt x 2 – 4 x + 2 = t ,
Khi đó (1) trở thành: t 2 + t – 6 = 0 ( 2 )
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 1 2 – 4 . 1 . ( - 6 ) = 25 > 0
⇒ (2) có hai nghiệm
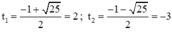
+ Với t = 2 ⇒ x 2 – 4 x + 2 = 2
⇔ x 2 – 4 x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x 2 – 4 x + 2 = - 3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ ’ = ( - 2 ) 2 – 1 . 5 = - 1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
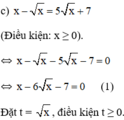
Khi đó (1) trở thành: t 2 – 6 t – 7 = 0 ( 2 )
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = 7 .
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
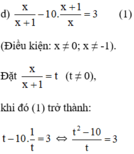
⇔ t 2 – 10 = 3 t ⇔ t 2 – 3 t – 10 = 0 ( 2 )
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = ( - 3 ) 2 - 4 . 1 . ( - 10 ) = 49 > 0
⇒ (2) có hai nghiệm:
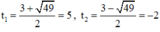
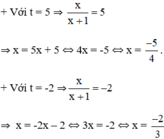
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm 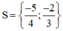
Giải pt sau (bằng 3 cách TẠO LŨY THỪA DƯỚI DẤU CĂN, ĐẶT ẨN PHỤ, DÙNG BĐT): \(x^2+6x-3=4x\sqrt{2x-1}\)
\(x^2+6x-3=4x\sqrt{2x-1}\left(1\right)\) ĐK: \(x\ge\frac{1}{2}\)
Đặt \(\sqrt{2x-1}=a\ge0\)
\(\Rightarrow6x-3=3a^2\)
=> (1) <=> x^2 +3a^2 = 4ax
<=> x^2 -4ax +3a^2 =0
<=> x^2 -ax - 3ax + 3a^2 =0
<=> x(x-a) -3a(x-a) =0
<=> (x-a) ( x-3a ) =0
\(\Leftrightarrow\orbr{\begin{cases}x=a\\x=3a\end{cases}}\)
TH1: x=a
\(\Rightarrow x=\sqrt{2x-1}\)\(\left(x\ge0\right)\)
\(\Leftrightarrow x^2=2x-1\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
<=> x=1 (tm)
TH2: x= 3a
\(\Rightarrow x=3\sqrt{2x-1}\left(x\ge0\right)\)
\(\Leftrightarrow x^2=18x-9\)
\(\Leftrightarrow x^2-18x+9=0\)
\(\Delta=288\)
=> pt có 2 nghiệm pb \(\orbr{\begin{cases}x=\frac{18+12\sqrt{2}}{2}=9+6\sqrt{2}\left(tm\right)\\x=\frac{18-12\sqrt{2}}{2}=9-6\sqrt{2}\left(tm\right)\end{cases}}\)
Vậy ...
Giải phương trình sau bằng cách đặt ẩn phụ:
\(\sqrt[4]{x}+\sqrt[4]{x+1}=\sqrt[4]{2x+1}\)
ĐK \(x\ge0\)
Đặt \(x=a,x+1=b\)
\(PT\Leftrightarrow a^4+b^4=\left(a+b\right)^4\)
<=> 4a3b+6a2b2+4ab3=0
<=> ab(2a2+3ab+2b2)=0
=>ab=0 (vì 2a2+3ab+2b2>0)
=>\(\orbr{\begin{cases}a=0\\b=0\end{cases}}\)<=>\(\orbr{\begin{cases}x=0\\x=-1\end{cases}}\)
Vậy.............................
Đặt ẩn phụ giải pt \(\sqrt{x+1}+\sqrt{5x}=\sqrt{4x-3}+\sqrt{2x+4}\)
ĐKXĐ: \(x\ge\dfrac{3}{4}\)
\(\Leftrightarrow\sqrt{5x^2+5x}=\sqrt{8x^2+10x-12}\) (1)
\(\Leftrightarrow\left(\sqrt{5x^2+5x}\right)^2=\left(\sqrt{8x^2+10x-12}\right)^2\)
\(\Leftrightarrow5x^2+5x=8x^2+10x-12\)
\(\Leftrightarrow5x^2+5x-\left(8x^2+10x-12\right)=8x^2+10x-12-\left(8x^2+10x-12\right)\)
\(\Leftrightarrow-3x^2-5x+12=0\)
\(\Leftrightarrow\left(-3x+4\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-3x+4=0\\x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-3x=-4\\x=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\left(OK\right)\\x=-3\left(loại\right)\end{matrix}\right.\)
Vậy tập nghiệm phương trình (1) là \(S=\left\{\dfrac{4}{3}\right\}\)