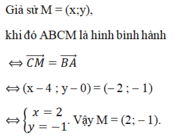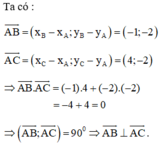trên mặt phẳng tọa độ Oxy, cho điểm A(2;4). hãy xác định vị trí tương đối của đường tròn (A;2) và các trục tọa độ
NP
Những câu hỏi liên quan
Trên mặt phẳng tọa độ Oxy, cho điểm A(2; 4). Hãy xác định vị trí tương đối của đường tròn (A; 2) và các trục tọa độ.
Do A(2; 4) nên A cách trục Ox 2 đơn vị, cách trục Oy 4 đơn vị
Khi đó đường tròn (A; 2) tiếp xúc với trục Ox và không giao nhau với trục Oy
Đúng 1
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho các điểm A(–1; 1); B(1; 2); C(4; 0). Tìm tọa độ điểm M sao cho ABCM là hình bình hành là:
A. M(2; 1)
B. M(2; –1)
C. M(–1; 2)
D. M(1; 2)
Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.
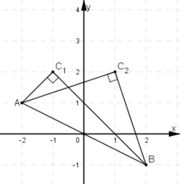
B đối xứng với A qua O ⇒ O là trung điểm của AB
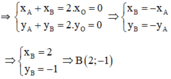
C có tung độ bằng 2 nên C(x; 2)
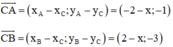
Tam giác ABC vuông tại C
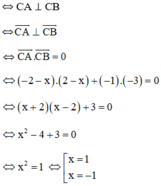
Vậy có hai điểm C thỏa mãn là C1(1; 2) và C2(–1; 2).
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho 2 điểm B(2;2), C(0;1). Tọa độ các điểm M nằm trên trục hoành thỏa MB = 2MC
\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A(1;3); B(-1;-2).Tìm tọa độ điểm M trên Oy sao cho A,B,D thẳng hàng
GẤP Ạ
Chắc là A,B,M thẳng hàng chứ?
Do M thuộc Oy nên tọa độ có dạng: \(M\left(0;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{BA}=\left(2;5\right)\\\overrightarrow{BM}=\left(1;m+2\right)\end{matrix}\right.\)
A, B, M thẳng hàng \(\Rightarrow\overrightarrow{BA}\) cùng phương \(\overrightarrow{BM}\)
\(\Rightarrow\dfrac{1}{2}=\dfrac{m+2}{5}\Rightarrow m=\dfrac{1}{2}\)
\(\Rightarrow M\left(0;\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho ba điểm A(2; 4), B(1; 2), C(6; 2). Chứng minh AB→ ⊥ AC→.
Trong mặt phẳng tọa độ Oxy cho 2 điểm B(2;2), C(0;1). Tọa độ các điểm M nằm trên trục hoành thỏa MB=2MC là
trên mặt phẳng tọa độ Oxy cho điểm M nằm trên parabol(P):y=\(x^2\)và điểm A(0;3). Xác định tọa độ điểm M sao cho độ dài AM ngắn nhất
Trong mặt phẳng tọa đọ Oxy cho hai điểm A (2,1) , B (-4,5)
a) Tìm tọa độ trung điểm I của đoạn thẳng AB
b) Tìm tọa độ điểm C trên trục hoành và tọa độ điểm D trên trục tung sao cho vecto AC= 2 vecto DB
Giúp mik vs mik đang cần gấp
a.
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{2-4}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{1+5}{2}=3\end{matrix}\right.\)
\(\Rightarrow I\left(-1;3\right)\)
b.
Do C thuộc trục hoành, gọi tọa độ C có dạng \(C\left(c;0\right)\)
Do D thuộc trục tung, gọi tọa độ D có dạng \(D\left(0;d\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(c-2;-1\right)\\\overrightarrow{DB}=\left(-4;5-d\right)\Rightarrow2\overrightarrow{DB}=\left(-8;10-2d\right)\end{matrix}\right.\)
Để \(\overrightarrow{AC}=2\overrightarrow{DB}\)
\(\Leftrightarrow\left\{{}\begin{matrix}c-2=-8\\-1=10-2d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}c=-6\\d=\dfrac{11}{2}\end{matrix}\right.\)
Vậy \(C\left(-6;0\right)\) và \(D\left(0;\dfrac{11}{2}\right)\)
Đúng 2
Bình luận (0)
trên mặt phẳng tọa độ oxy cho A (5;-3) B(2;4) C(1;5) .tìm tọa độ điểm D sao cho ABCD là hình bình hành
\(\overrightarrow{AB}=\left(-3;7\right)\)
\(\overrightarrow{DC}=\left(1-x_D;5-y_D\right)\)
Để ABCD là hbh thì
\(\left\{{}\begin{matrix}1-x_D=-3\\5-y_D=7\end{matrix}\right.\Leftrightarrow D\left(2;-2\right)\)
Đúng 1
Bình luận (0)