cho tam giác ABC có BC=a , AC=b AB=c có 3B+2C=180 độ chứng minh b+c<=5/4a
VN
Những câu hỏi liên quan
CHO tam giác ABC có AB=c, AC=b, BC=a
Chứng minh: Với B>90 độ =>\(b^2=a^2+c^2+2ac.\cos\left(180^o-B\right)\)
Cái này là công thức hàm số cos nha
Hàm số cos theo em tới lớp 11 12 luôn nha ( bài tập vật lí 11 12 )
Lên lớp 10 sẽ học
Còn chứng minh quên rồi
Cái này được suy ra từ định lí hàm số cos:
trong \(\Delta ABC\)thì \(b^2=a^2+c^2-2ac.\cos B\)
Với \(\Delta ABC\)có góc \(B\)tù thì \(\cos B=-\cos\left(180-\widehat{B}\right)\)
nên khi đó ta có thể viết lại:
\(b^2=a^2+c^2-2ac\left[-\cos\left(180-\widehat{B}\right)\right]\)\(\Rightarrow b^2=a^2+c^2+2ac.\cos\left(180^o-\widehat{B}\right)\)
Dăm ba mấy cái định lý hàm số cos em chẳng hiểu gì cả :((
Từ A kẻ \(AH\perp BC\left(H\in BC\right)\)
Khi đó biến đổi qua 1 số bước đơn giản ta được:
\(b^2=AC^2=AH^2+CH^2\)
\(=\left(AB^2-HB^2\right)+\left(BC+BH\right)^2\)
\(=\left(c^2-BH^2\right)+\left(a+BH\right)^2\)
\(=c^2-BH^2+a^2+2\cdot a\cdot BH+BH^2\)
\(=a^2+c^2+2\cdot a\cdot BH\)
\(=a^2+c^2+2ac\cdot\cos\widehat{HBA}\)
\(=a^2+c^2+2ac\cdot\cos\left(180^0-\widehat{ABC}\right)\)
\(=a^2+c^2+2ac\cdot\cos\left(180^0-\widehat{B}\right)\)
Vậy khi góc B > 90 độ thì \(b^2=a^2+c^2+2ac\cdot\cos\left(180^0-\widehat{B}\right)\)
Cho tam giác ABC có độ dài 3 cạnh là a, b, c thỏa mãn: \(\dfrac{ab}{b+c}+\dfrac{bc}{c+a}+\dfrac{ac}{a+b}=\dfrac{ac}{b+c}+\dfrac{ab}{c+a}+\dfrac{bc}{a+b}\). Chứng minh: Tam giác ABC cân
Cho tam giác ABC có độ dài 3 cạnh là a, b, c thỏa mãn: \(\dfrac{ab}{b+c}+\dfrac{bc}{a+c}+\dfrac{ac}{a+b}=\dfrac{ac}{b+c}+\dfrac{ab}{a+c}+\dfrac{bc}{a+b}\). Chứng minh tam giác ABC cân
\(\Leftrightarrow ab\left(\dfrac{1}{b+c}-\dfrac{1}{a+c}\right)+bc\left(\dfrac{1}{a+c}-\dfrac{1}{a+b}\right)+ca\left(\dfrac{1}{a+b}-\dfrac{1}{b+c}\right)=0\)
\(\Leftrightarrow\dfrac{ab\left(a-b\right)}{\left(b+c\right)\left(a+c\right)}+\dfrac{bc\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{ca\left(c-a\right)}{\left(a+b\right)\left(b+c\right)}=0\)
\(\Leftrightarrow\dfrac{ab\left(a^2-b^2\right)+bc\left(b^2-c^2\right)+ca\left(c^2-a^2\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)\left(a+b+c\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\) hay tam giác cân
Đúng 1
Bình luận (0)
Cho tam giác ABC có A = 180°– 3C a) Chứng minh rằng B = 2C. Cho B = 80°, tính số do các góc của tam giác. b) Vẽ tia phân giác của góc B cắt AC tại E. Qua E kẻ đường song song với BC, cắt AB tại D. Chứng minh rằng ED là tia phân giác của góc AEB. Huhu mọi ngừi cố gắng giúp mình nha, thanks nè ❤️❤️❤️
\(a,\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180\) mà \(\widehat{A}=180-3\widehat{C}\)
\(\Rightarrow\widehat{B}+\widehat{C}=180-\widehat{A}=3C\\ \Rightarrow\widehat{B}=2\widehat{C}\)
Thay \(\widehat{B}=80\Rightarrow\widehat{C}=\dfrac{80}{2}=40\Rightarrow\widehat{A}=180-3\cdot40=60\)
\(b,\) Ta có \(DE//BC\)
\(\Rightarrow\widehat{EBC}=\widehat{DEB}\left(SLT\right)\)
Ta có \(\widehat{AEB}=\widehat{C}+\widehat{EBC}=\widehat{C}+\dfrac{1}{2}\widehat{B}=\widehat{C}+\dfrac{1}{2}\cdot2\widehat{C}=2\widehat{C}=\widehat{B}\)
(vì \(\widehat{AEB}\) là góc ngoài \(\Delta EBC\))
\(\Rightarrow\widehat{AED}+\widehat{DEB}=\widehat{ABE}+\widehat{EBC}\)
Mà \(\widehat{EBC}=\widehat{DEB}\left(cmt\right)\)
\(\Rightarrow\widehat{AED}=\widehat{ABE}\)
Mà \(\widehat{EBC}=\widehat{ABE}\left(GT\right)\)
\(\Rightarrow\widehat{DEB}=\widehat{AED}\)
Vậy \(ED\) là phân giác \(\widehat{AEB}\)
Đúng 2
Bình luận (0)
Câu 4(3 điểm) Cho tam giác ABC có AB = 6 cm; AC = 8cm BC = 10cm a) Chứng minh ABC là tam giác vuông. b) Tĩnh angle B 2C; và đường cao AH. c) Lấy M bất kỳ trên cạnh BC. Gọi P; Q lần lượt là hình chiếu của M trên AB; AC. Hỏi M ở vị trí nào thì PO có độ dài nhỏ nhất.
cho tam giác abc có góc a bằng 90 độ ab bằng ac gọi k là trung điểm của bc a chứng minh tam giác akb bằng tam giác ac b chứng minh ak vuông góc với bc c từ c vẽ đường vuông góc với bc tại c cắt đường thẳng ab tại a chứng minh ac // ak
Cho tam giác ABC có BC = a, AC = b, AB = c và a2 = bc. Chứng minh rằng tam giác ABC đồng dạng với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.
a. Cho tam giác ABC có góc B = 60 độ. Cạnh Bc = 1/2 cạnh AB. Chứng minh góc C = 90 đo.
b. Tam giác ABC có góc B =60 độ, BC= 2dm. AB = 3dm. Gọi D là trung đieemr của BC. Chứng minh AD=AC
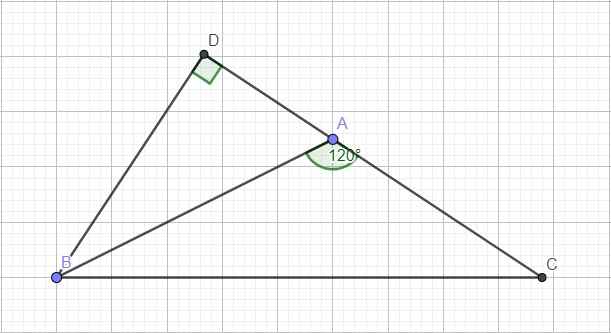
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)