Cho hình vuông ABCD cạnh a . tính \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình vuông ABCD cạnh a . Tính giá trị các biểu thức sau:
a) \(\overrightarrow{AB}.\overrightarrow{AC}\)
b)\(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
c)\(\overrightarrow{AB}.\overrightarrow{BD}\)
d) \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)\)
e) \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
a, \(AC=\dfrac{AB}{sin45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a\sqrt{2}.cos45^o=a^2\)
b, \(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=\overrightarrow{AC}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{AC}.\overrightarrow{BD}+\overrightarrow{AC}.\overrightarrow{BC}\)
\(=AC.BD.cos90^o+AC.AD.cos45^o\)
\(=a\sqrt{2}.a\sqrt{2}.0+a\sqrt{2}.a.\dfrac{\sqrt{2}}{2}=a^2\)
c, \(\overrightarrow{AB}.\overrightarrow{BD}=AB.BD.cos135^o=-a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=-a^2\)
d, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{BC}.\left(\overrightarrow{AD}+\overrightarrow{BD}\right)\)
\(=\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{BC}.\overrightarrow{BD}\)
\(=AD^2+BC.BD.cos45^o\)
\(=a^2+a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=2a^2\)
e, \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
\(=\left(\overrightarrow{AC}+\overrightarrow{AC}\right)\left(\overrightarrow{DB}+\overrightarrow{DB}\right)\)
\(=4.\overrightarrow{AC}.\overrightarrow{DB}=4.AC.DB.cos90^o=0\)
Cho hình vuông ABCD cạnh a. Tính \(\left|\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right|\)
Ta có: (vectơ AB + vectơ AD) + vectơ AC
= vectơ AC + vectơ AC
= 2 vectơAC
=> | vectơ AB + vectơ AC + vectơ AD| = 2 vectơAC = 2a căn 2
Cho hình vuông ABCD cạnh a, O=\(AB\cap BD\). Tính:
\(\left|\overrightarrow{OA}-\overrightarrow{CB}\right|\),\(\left|\overrightarrow{AB}+\overrightarrow{DC}\right|\), \(\left|\overrightarrow{CD}-\overrightarrow{DA}\right|\)
\(\left|\overrightarrow{OA}-\overrightarrow{CB}\right|=\left|\overrightarrow{OA}+\overrightarrow{BC}\right|=\left|\overrightarrow{OA}+\overrightarrow{AD}\right|=\left|\overrightarrow{OD}\right|=OD=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\)
\(\left|\overrightarrow{AB}+\overrightarrow{DC}\right|=\left|\overrightarrow{AB}+\overrightarrow{AB}\right|=2\left|\overrightarrow{AB}\right|=2AB=2a\)
\(\left|\overrightarrow{CD}-\overrightarrow{DA}\right|=\left|\overrightarrow{CD}+\overrightarrow{AD}\right|=\left|\overrightarrow{BA}+\overrightarrow{AD}\right|=\left|\overrightarrow{BD}\right|=BD=a\sqrt{2}\)
Cho hình vuông ABCD cạnh a; O=\(AB\cap BD\). Tính:
\(\left|\overrightarrow{OA}-\overrightarrow{CB}\right|\), \(\left|\overrightarrow{AB}+\overrightarrow{DC}\right|\), \(\left|\overrightarrow{CD}-\overrightarrow{DA}\right|\)
1.Cho hình vuông ABCD cạnh a . Tính \(\left|\overrightarrow{AD}+\overrightarrow{3AB}\right|\) theo a
2. Cho tam giác ABC đều cạnh a. M là trung điểm BC . Tính \(\left|\overrightarrow{MA}+3\overrightarrow{MB}+\overrightarrow{MC}\right|\)theo a
3. Cho tam giác ABC đều cạnh a có G là trọng tâm . Tính \(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|\)theo a
Giups mik vs ạ . Tks
1.
Đặt \(P=\left|\overrightarrow{AD}+3\overrightarrow{AB}\right|\Rightarrow P^2=AD^2+9AB^2+6\overrightarrow{AD}.\overrightarrow{AB}\)
\(=AD^2+9AB^2=10AB^2=10a^2\)
\(\Rightarrow P=a\sqrt{10}\)
2.
Tam giác ABC đều nên AM là trung tuyến đồng thời là đường cao \(\Rightarrow AM\perp BM\)
\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(BM=\dfrac{a}{2}\)
\(T=\left|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)
\(\Rightarrow T^2=MA^2+4MB^2+4\overrightarrow{MA}.\overrightarrow{MB}=MA^2+4MB^2\)
\(=\left(\dfrac{a\sqrt{3}}{2}\right)^2+4\left(\dfrac{a}{2}\right)^2=\dfrac{7a^2}{4}\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(T=\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\right|\)
\(=\left|\dfrac{4}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\right|\Rightarrow T^2=\dfrac{16}{9}AB^2+\dfrac{4}{9}AC^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{20}{9}AB^2-\dfrac{16}{9}AB^2.cos60^0=\dfrac{20}{9}a^2-\dfrac{16}{9}a^2.\dfrac{1}{2}=\dfrac{4}{3}a^2\)
\(\Rightarrow T=\dfrac{2a}{\sqrt{3}}\)
Cho hình vuông ABCD tâm có cạnh bằng a, tâm O. M là điểm thỏa mãn hệ thức \(\left|\overrightarrow{MA}+\overrightarrow{MC}+2\overrightarrow{MB}+2\overrightarrow{OC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\) Khoảng cách lớn nhất từ M đến D bằng?
Gọi N là trung điểm BC
\(\left|\overrightarrow{MA}+\overrightarrow{MC}+2\overrightarrow{MB}+2\overrightarrow{OC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MO}+2\overrightarrow{MB}+2\overrightarrow{OC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MC}+2\overrightarrow{MB}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow4\left|\overrightarrow{MN}\right|=\left|\overrightarrow{BD}\right|\)
\(\Rightarrow\left|\overrightarrow{BD}\right|=4\left|\overrightarrow{MN}\right|=4\left|\overrightarrow{DN}+\overrightarrow{MD}\right|\ge4MD-4DN\)
\(\Rightarrow4MD\le BD+4DN\)
\(\Leftrightarrow MD\le\dfrac{BD+4DN}{4}=\dfrac{a\sqrt{2}+2a\sqrt{5}}{4}=\dfrac{2\sqrt{5}+\sqrt{2}}{4}a\)
Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:
\(\overrightarrow {AB} .\overrightarrow {AD} ,\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} ,\overrightarrow {AC} .\overrightarrow {BD} \)
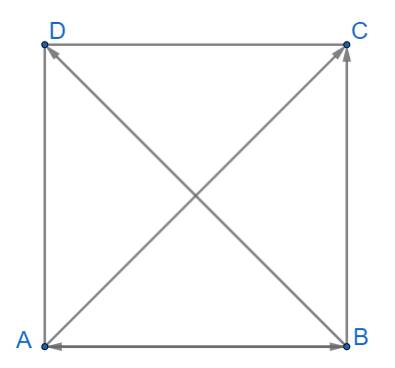
Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) \(AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
+) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2.\cos 45^\circ = a^2\)
+) \(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ = - {a^2}\)
+) \(AC \bot BD \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\)
Chú ý
\(\overrightarrow {a} \bot \overrightarrow {b} \Leftrightarrow \overrightarrow {a} .\overrightarrow {b} = 0\)
Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?
A. \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {45^o}\)
B. \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^o}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = {a^2}\)
C. \(\overrightarrow {AC} .\overrightarrow {BD} = {a^2}\sqrt 2 \)
D. \(\overrightarrow {BA} .\overrightarrow {BD} = - {a^2}\)
Tham khảo:
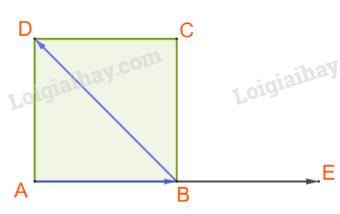
A. Ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {BE} ,\overrightarrow {BD} } \right) = {135^o} \ne {45^o}.\) Vậy A sai.
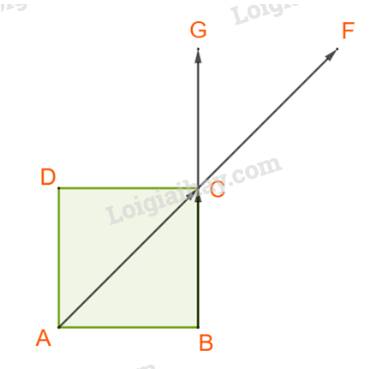
B. Ta có: \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {CF} ,\overrightarrow {CG} } \right) = {45^o}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = AC.BC.\cos {45^o} = a\sqrt 2 .a.\frac{{\sqrt 2 }}{2} = {a^2}.\)
Vậy B đúng.
Chọn B
C. Dễ thấy \(AC \bot BD\) nên \(\overrightarrow {AC} .\overrightarrow {BD} = 0 \ne {a^2}\sqrt 2.\) Vậy C sai.
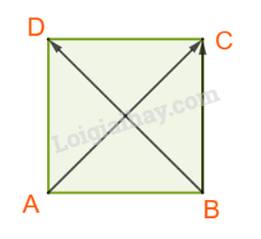
D. Ta có: \(\left( {\overrightarrow {BA} .\overrightarrow {BD} } \right) = {45^o}\) \( \Rightarrow \overrightarrow {BA} .\overrightarrow {BD} = BA.BD.\cos {45^o} = a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2} \ne - {a^2}.\) Vậy D sai.
cho hình chữ nhật ABCD có AB=3a, AD=a. Điểm M là trung điểm của AM. Tính véc tơ tổng:
a)\(\left|\overrightarrow{AM}+\overrightarrow{AB}\right|\)
b)\(\left|\overrightarrow{AB}+\overrightarrow{CD}\right|\)
c) Cho điểm N thuộc AB sao cho AN = AD. Tính véc tơ tổng \(\left|\overrightarrow{DN}+\overrightarrow{BN}\right|\)
** M là trung điểm của AB đúng không bạn?
a.
\(|\overrightarrow{AM}+\overrightarrow{AB}|=|\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AB}|=\frac{3}{2}|\overrightarrow{AB}|=\frac{3}{2}.3a=\frac{9a}{2}\)
b.
\(|\overrightarrow{AB}+\overrightarrow{CD}|=|\overrightarrow{AB}+\overrightarrow{BA}|=|\overrightarrow{0}|=0\)
c.Trên $CD$ lấy $K$ sao cho $CK=a$. Khi đó:
\(|\overrightarrow{DN}+\overrightarrow{BN}|=|\overrightarrow{DN}+\overrightarrow{KD}|=|\overrightarrow{KN}|=KN=\sqrt{a^2+a^2}=\sqrt{2}a\)
Cho hình thoi ABCD cạnh a, \(\widehat{BCD}\)= 60o . O là giao điểm của AC và BD . Tính \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|,\left|\overrightarrow{CB}+\overrightarrow{DC}\right|\)