Tính giá trị của :
sin(10o)+sin(20o)+...+sin(70o)+sin(80o)
Ai giải được mình cho 1 t.i.c.k nhoa!
1) Giai phuong trinh:
a) Sin ( 4x + 10o) = Sin ( x - 20o )
\(\Leftrightarrow\left[{}\begin{matrix}4x+10^0=x-20^0+k360^0\\4x+10^0=200^0-x+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=-30^0+k360^0\\5x=190^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-10^0+k120^0\\x=38^0+k72^0\end{matrix}\right.\) (\(k\in Z\))
So sánh: sin 20o và sin 70o
Vì 20o < 70o nên sin 20o < sin70o (góc tăng, sin tăng)
Cho cos α = 1 3 . Tính giá trị của biểu thức P = sin 3 a - sin a sin 2 a
![]()
![]()

![]()
Chọn A.
Áp dụng công thức biến đổi tổng thành tích và công thức nhân đôi; ta có
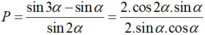

Cho cotx=2 . Tính giá trị của biểu thức B= sin^ 2 x-2 sin x.cos x-1 / 5cos^2 x + sin^2 x - 3
cotx=2
=>cosx=2*sin x
\(1+cot^2x=\dfrac{1}{sin^2x}\)
=>\(\dfrac{1}{sin^2x}=1+4=5\)
=>\(sin^2x=\dfrac{1}{5}\)
\(B=\dfrac{sin^2x-2\cdot sinx\cdot2\cdot sinx-1}{5\cdot4sin^2x+sin^2x-3}=\dfrac{-3sin^2x-1}{21sin^2x-3}\)
\(=\dfrac{-\dfrac{3}{5}-1}{\dfrac{21}{5}-3}=-\dfrac{8}{5}:\dfrac{6}{5}=-\dfrac{4}{3}\)
\(cotx=2\Rightarrow tanx=\dfrac{1}{2}\)
\(B=\dfrac{sin^2x-2sinx.cosx-1}{5cos^2x+sin^2x-3}\)
\(\Leftrightarrow B=\dfrac{tan^2x-2tanx-\dfrac{1}{cos^2x}}{5+tan^2x-\dfrac{3}{cos^2x}}\)
\(\Leftrightarrow B=\dfrac{tan^2x-2tanx-1-tan^2x}{5+tan^2x-3-3tan^2x}\)
\(\Leftrightarrow B=\dfrac{-2tanx-1}{2-2tan^2x}\)
\(\Leftrightarrow B=\dfrac{-2.\dfrac{1}{2}-1}{2-2.\dfrac{1}{4}}=\dfrac{-2}{\dfrac{3}{2}}=-\dfrac{4}{3}\)
Cho cot x = 2 . Tính giá trị của biểu thức B= sin^ 2 x-2 sin x.cos x-1/5cos^2 x + sin^2 x - 3
cot x=2>0
=>sin x và cosx cùng dấu
=>sinx*cosx>0
\(1+cot^2x=\dfrac{1}{sin^2x}=1+4=5\)
=>sin^2x=1/5
=>cos^2x=4/5
\(B=\dfrac{1}{5}-2\cdot sinx\cdot cosx-\dfrac{1}{5}\cdot\dfrac{4}{5}+\dfrac{1}{5}-3\)
\(=\dfrac{2}{5}-\dfrac{4}{25}-3-2\cdot\dfrac{1}{\sqrt{5}}\cdot\dfrac{2}{\sqrt{5}}\)
\(=\dfrac{10}{25}-\dfrac{4}{25}-\dfrac{75}{25}-2\cdot\dfrac{2}{5}=\dfrac{-69}{25}-\dfrac{4}{5}=\dfrac{-89}{25}\)
1. Cho biết \(cosx=\dfrac{3}{4}\). Tính giá trị của biểu thức \(P=sin^22x\).
2. Giải phương trình \(cos2x-sin\left(x+\dfrac{\pi}{3}\right)=0\)
1: \(P=sin^22x=1-cos^22x\)
\(=1-\left(cos2x\right)^2\)
\(=1-\left(2cos^2x-1\right)^2\)
\(=1-\left(2\cdot\dfrac{9}{16}-1\right)^2\)
\(=1-\left(\dfrac{9}{8}-1\right)^2=1-\left(\dfrac{1}{8}\right)^2=\dfrac{63}{64}\)
2:
\(cos2x-sin\left(x+\dfrac{\Omega}{3}\right)=0\)
=>\(sin\left(x+\dfrac{\Omega}{3}\right)=cos2x=sin\left(\dfrac{\Omega}{2}-2x\right)\)
=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=\dfrac{\Omega}{2}-2x+k2\Omega\\x+\dfrac{\Omega}{3}=\Omega-\dfrac{\Omega}{2}+2x+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3x=\dfrac{\Omega}{6}+k2\Omega\\-x=\dfrac{1}{6}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{18}+\dfrac{k2\Omega}{3}\\x=-\dfrac{1}{6}\Omega-k2\Omega\end{matrix}\right.\)
Tính giá trị biểu thức M= sin²42⁰+sin²43⁰+sin²44⁰+sin²45⁰+sin²46⁰+sin²47⁰+sin²48⁰ Giúp em với mn ;-;
Các góc dưới đây đều là độ:
Sử dụng đẳng thức \(sina=cos\left(90^0-a\right)\) và \(sin^2a+cos^2a=1\):
\(M=sin^242+sin^243+sin^244+sin^245+cos^2\left(90-46\right)+cos^2\left(90-47\right)+cos^2\left(90-48\right)\)
\(=sin^242+sin^243+sin^244+sin^245+cos^244+cos^243+cos^242\)
\(=\left(sin^242+cos^242\right)+\left(sin^243+cos^243\right)+\left(sin^244+cos^244\right)+\left(\dfrac{\sqrt{2}}{2}\right)^2\)
\(=1+1+1+\dfrac{1}{2}=\dfrac{7}{2}\)
Giúp mình với các bạn ơi!!!!!!!!!!!!!!
Cho sina*cosa=0.22. Tính giá trị của biểu thức M=\(\sin^3a+\cos^3a-2.\sin a.\cos a\)