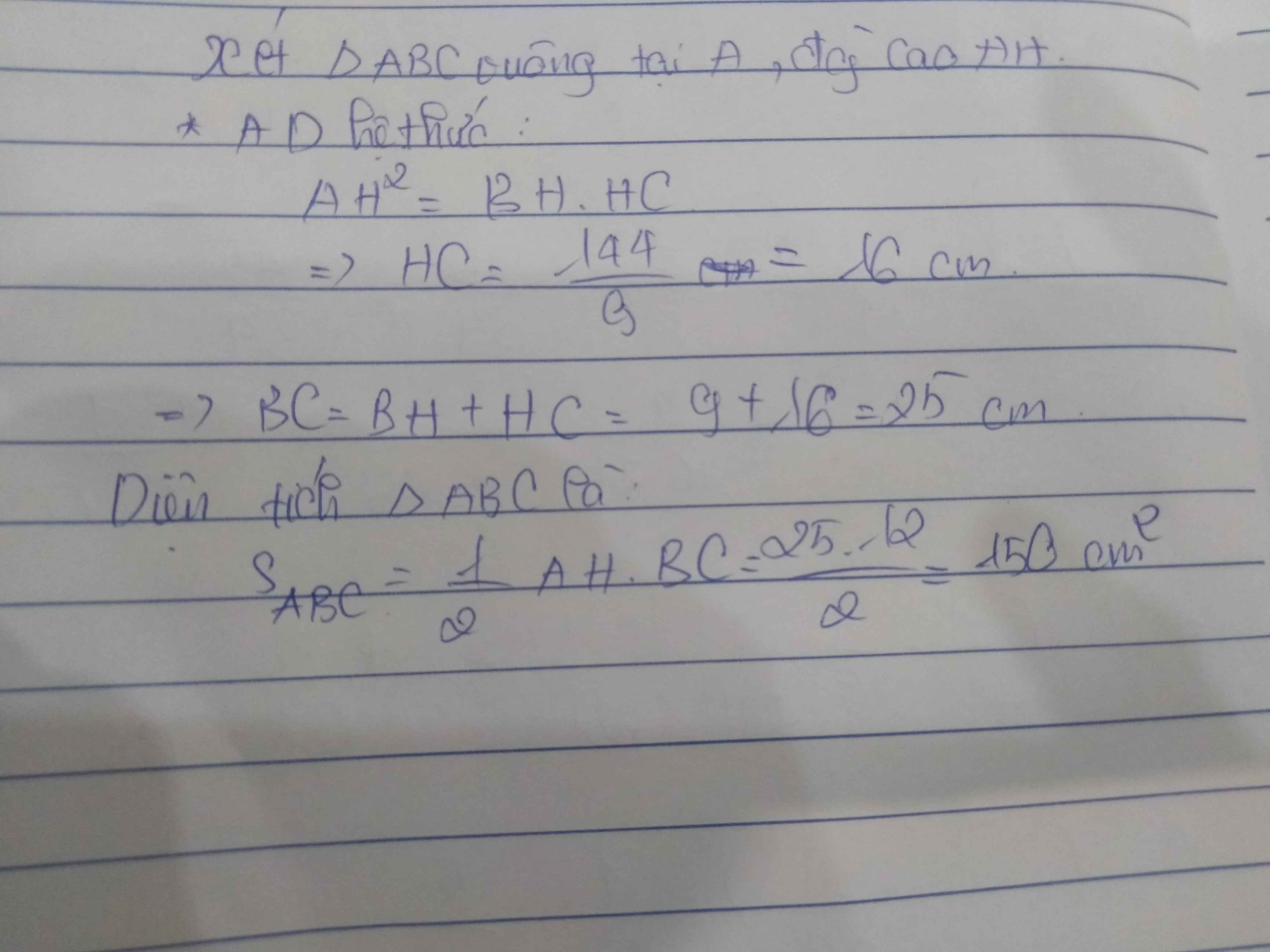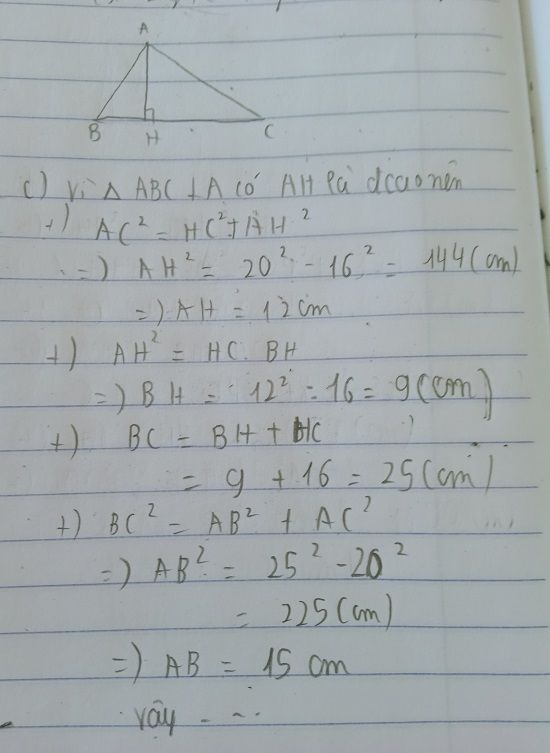Tam giác ABC vuông tại A , đường cao AH biết AC=20 cm , AH=12cm .Tính diện tích ABC
NA
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A , đường cao AH biết AH = 12cm , HC=16 cm tính diện tích tam giác ABC
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=HB.HC\Rightarrow HB=\dfrac{AH^2}{HC}=\dfrac{144}{16}=9\)cm
-> BC = HB + HC = 9 + 16 = 25 cm
Diện tích tam giác ABC là : \(S_{ABC}=\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.12.25=150\)cm2
Đúng 1
Bình luận (0)
Áp dụng hệ thức lượng:
\(AB^2=BH.CH\Rightarrow BH=\dfrac{AH^2}{CH}=9\left(cm\right)\)
\(\Rightarrow BC=BH+CH=25\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=150\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=\dfrac{144}{16}=9\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=150\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH24 cm và HC18 cm.
Tính: BH, ,BC,AC,AB và diện tích tam giác ABC
Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB 12 cm và BC20 cm.
Tính: BH, ,AC,HC,AH và diện tích tam giác ABC
Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB3 cm và AC4 cm.
Tính: BH, ,BC,HC,AH và diện tích tam giác ABC
Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC15 cm và AH 12 cm.
Tính: BH, ,BC,A...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A, AB < AC, đường cao AH. Biết AH = 6 cm, diện tích tam giác ABC = 37,5 cm vuông. Tính AB, AC
Vì SABC=37,5=>AH.BC=75=>BC=12,5
Đặt cạnh CH=x
=>HB=12,5-x
Áp dụng hệ thức 2 vào tam giác abc
AH2=BH.CH
<=>62=x(12,5-x)
<=>36=12,5x-x2
<=>x2-12,5x+36=0
<=>(x-6,25)2=3
..............tìm x sau đó thay vào tìm ab,ac
Đúng 0
Bình luận (0)
Cho Tam giác ABC vuông tại A , đường cao AH . Tính diện tích Tam giác ABC , biết AH = 12cm , BH= 9cm
Áp dụng HTL trong tam giác vuông ABC :
\(AH^2=BH\cdot CH\)
\(\Rightarrow CH=\dfrac{12^2}{9}=16\left(cm\right)\)
\(BC=BH+CH=9+16=25\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot12\cdot25=150\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{AH^2}{HB}=\dfrac{12^2}{9}=16\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=150\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC, biết AH = 12cm, BH = 9cm
Cho tam giác ABC vuông tại A, đường cao AH .
a) Biết AH = 12cm ,CH = 5cm.Tính AC , AB , BC , BH
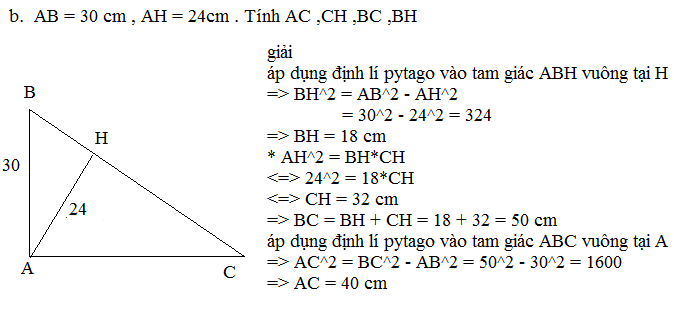
b) Biết AB = 30 cm, AH = 24 cm. Tính AC ,CH ,BC ,BH
c) Biết AC = 20 cm , CH = 16 cm. Tính AB ,AH,BC,BH
d) Biết AB = 6 cm , BC = 10 cm . Tính AC, AH, BH, CH
e) Biết BH =9 cm, CH = 16 cm . Tính AC , AB, BC, AH
Giúp mìn với ạ, cảm ơn nhìu
d) \(AC=\sqrt{BC^2-AB^2}=8\)
\(AH=\dfrac{AB.AC}{BC}=4,8\)
\(BH=\sqrt{AB^2-AH^2}=3,6\)
\(CH=BC-BH=6,4\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 2: Cho tam giác ABC vuông tại A có AB=12cm AC=16cm ve đường cao AH A) CM tam giác ABC đồng dạng tam giác HBA B) tính Bc, AH, BH C) Trên AH lấy điểm K sao cho AK=3,6cm. Từ K đường thẳng // BC cắt Ab và AC lần lượt tại M và N. Tính diện tích tứ giác BMNC
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC∼ΔHBA(g-g)
Đúng 0
Bình luận (0)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Vậy: BC=20cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 5cm, AC = 12cm, đường cao AH. a) Tính BC, BH, AH. b) Gọi AM là đường trung tuyến của tam giác ABC, tính diện tích tam giác AHM
\(a,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\\ HTL:\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{13}\left(cm\right)\\BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\end{matrix}\right.\\ b,AM=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\left(trung.tuyến.ứng.cạnh.huyền\right)\\ \Rightarrow HM=\sqrt{AM^2-AH^2}=\dfrac{119}{26}\left(cm\right)\\ \Rightarrow S_{AHM}=\dfrac{1}{2}AH\cdot HM=\dfrac{1}{2}\cdot\dfrac{60}{13}\cdot\dfrac{119}{26}=\dfrac{1785}{169}\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Giúp tớ với 1. Cho tam giác ABC có đường cao AH. Gọi M, N là hình chiếu của H trên AB, AC. Chứng minh: tam giác ABC đồng dạng với tam giác ANM2.Cho tam gíac ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC, biết AH 12cm , BH 9cm . 3.Cho tam giác ABC, biết BC 7,5cm , CA 4,5 cm , AB 6 cm . a) Tam giác ABC là tam giác gì ? Tính đường cao AH của tam giác ABC; b) Tính độ dài các đoạn BH, CH4.. Cho hình bình hành ABCD có góc A nhọn. Gọi I, K lần lượt là hình chiếu của B, D trên đường chéo...
Đọc tiếp
Giúp tớ với
1. Cho tam giác ABC có đường cao AH. Gọi M, N là hình chiếu của H trên AB, AC. Chứng minh: tam giác ABC đồng dạng với tam giác ANM
2.Cho tam gíac ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC, biết AH= 12cm , BH= 9cm .
3.Cho tam giác ABC, biết BC =7,5cm , CA =4,5 cm , AB= 6 cm . a) Tam giác ABC là tam giác gì ? Tính đường cao AH của tam giác ABC; b) Tính độ dài các đoạn BH, CH
4.. Cho hình bình hành ABCD có góc A nhọn. Gọi I, K lần lượt là hình chiếu của B, D trên đường chéo AC. Gọi M và N lần lượt là các hình chiếu của C trên đường thẳng AB, AD. Chứng minh:
a) AK= IC .
b) Tứ giác BIDK là hình bình hành.
c) 2 AC AD AN AB AM